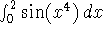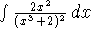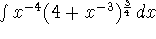Next: About this document
Up: MA1022 Lab 1 -
Previous: Integration using Maple
- For each function listed, do the following.
Plot each function to verify that it is non-negative over the
interval in question.
Determine the area under the curve using the int command.
Choose one of the three rectangular approximations leftsum,
rightsum or middlesum and determine the minimum number of
subintervals required so that the approximation agrees with the
integral to the fourth decimal place. Don't use the same rectangular
approximation method for every part; please use each method at least
once.
-
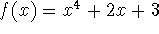 on the interval [0,5].
on the interval [0,5].
-
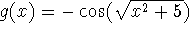 on the interval [-4,4].
on the interval [-4,4].
-
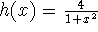 on the interval [-1,1].
on the interval [-1,1].
- Use the Maple int command to work the following problems. Explain your ``setup" for each problem.
- Find the average value of the function
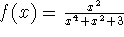 on the interval [-5,-1].
on the interval [-5,-1].
- Find the area between
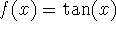 and
and 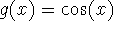 on the interval
on the interval 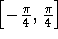 .
.
- Find the general anti-derivative of
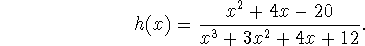
- Let
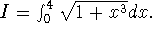
- Approximate I by
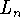 for n = 20, 60 and 100.
for n = 20, 60 and 100.
Approximate I by 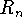 for n = 20, 60 and 100.
for n = 20, 60 and 100.
Approximate I by 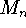 for n = 20, 60 and 100.
for n = 20, 60 and 100.
- Write a paragraph summarizing your experience in this problem. (Feel free to run additional lines of Maple if you need to.) What approximation method seems to be the most accurate? Include at least one more insight you have gained from this exercise.
- Use Maple to compute the following definite and indefinite integrals.
-
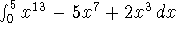
-
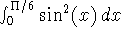
-
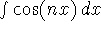 , where n is a positive constant.
, where n is a positive constant.
-
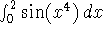
-
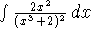
-
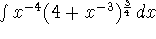
Roxanne Tisch
Thu Mar 27 08:41:19 EST 1997
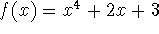 on the interval [0,5].
on the interval [0,5].
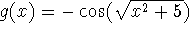 on the interval [-4,4].
on the interval [-4,4].
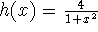 on the interval [-1,1].
on the interval [-1,1].
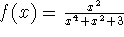 on the interval [-5,-1].
on the interval [-5,-1].
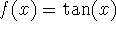 and
and 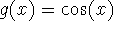 on the interval
on the interval 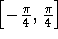 .
.
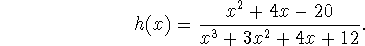
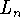 for n = 20, 60 and 100.
for n = 20, 60 and 100.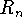 for n = 20, 60 and 100.
for n = 20, 60 and 100.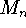 for n = 20, 60 and 100.
for n = 20, 60 and 100.
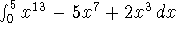
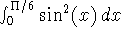
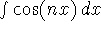 , where n is a positive constant.
, where n is a positive constant.