Exercises

1. This exercise is intended to familiarize you with the procedures revolve, RevInt, LeftDisk and LeftInt as an approach to approximating the volume of a solid of revolution using the disk method. Apply the four commands as listed above to the function f defined by 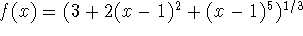on the interval [0,2] with n=10. Your answer should include the two numerical values and references to the two 3-dimensional plots.
2. A torus - a solid shaped like a doughnut - is generated by revolving a circle about an axis that does not intersect the circle. By rotating the circle 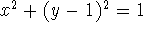about the line y = 3, print a plot of the torus which depicts its doughnut-like image and compute its volume. Your answer should include the numerical value for the volume and a reference to the 3-dimensional plot.
3. How would you generalize the formula given in the background to find the volume of a solid generated by revolving the area between a segment of the graph of a function and an arbitrary line parallel to the x-axis?
4. Design a drinking glass by revolving a suitable function about the x-axis. In your report, give the function, a three dimensional plot of your glass and calculate the volume of the liquid filled portion. You will be graded on the utility and elegance of your design.