


Next: About this document ...
Up: Labs and Projects for
Previous: Decimal Place Accuracy
- 1.
- Plot the function. Using left and right sum commands, find which command will be the most accurate, then use this command and find the minimum number of subdivisions necessary for two decimal place accuracy for the area under the curve.
- (a)
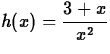 , x = 1..5
, x = 1..5
- (b)
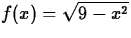 , x = 0..3
, x = 0..3
- (c)
- e(x) = 5x-8, x = -1..4
- 2.
- Consider the function e(x)=5x-8 on the interval [-1,4]. Verify that the middlesum command gives the exact value for the area independant of the number of subintervals you specify. Please explain this using your geometry or trigonometry knowledge.
- 3.
- Plot each of the following functions. Experiment with the rightsum and leftsum commands as well as the rightbox and leftbox commands on the following functions, discover why the rightsum and leftsum are equal.
- (a)
- j(x) = -7x4 + 13x3 - x + 10, x = -0.83177883..2
- (b)
- m(x) = x3 - 6x2 + 5x + 12, x = -1..3
- (c)
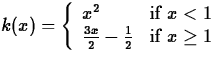 , x = -2..3
, x = -2..3
The Maple command to define this function is given below.
> k:=x->piecewise(x<1, x^2,3/2*x-1/2);
Christine M Palmer
3/24/1998
![]()
![]()
![]()
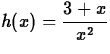 , x = 1..5
, x = 1..5
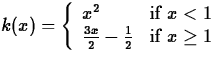 , x = -2..3
, x = -2..3