


Next: About this document ...
Up: Labs and Projects for
Previous: Riemann Sums
- 1.
- Consider
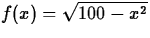 on the interval [0,10].
on the interval [0,10].
- (a)
- For n = 8,16, and 32, approximate the area under the curve by
using each of the left endpoint rule, right endpoint rule and midpoint
rule.
- (b)
- Use your knowledge of geometry to obtain the exact value of the
area. Which of the three rules seems to give the best approximation
to the area for a given n? Explain.
- (c)
- What is the smallest n for which the midpoint rule
approximation is accurate to two decimal places, i.e, that
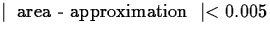 ? Justify your answer by
showing that your n does work and that n - 1 does not work.
Comment as needed on your work.
? Justify your answer by
showing that your n does work and that n - 1 does not work.
Comment as needed on your work.
- (d)
- Check the accuracy of the left endpoint and right endpoint rules
when n = 9900. Does either one give an approximation with 2-place
accuracy? Which of the three rules seems to be better? Why?
- 2.
- Consider
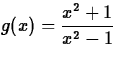 on the
interval [2,5].
on the
interval [2,5].
- (a)
- Use the appropriate box command with 9 rectangles to display an upper
sum approximation to the area under the curve. Explain your choice of
box command.
- (b)
- For n = 20,40 and 80, approximate the area under the curve
with an upper sum.
- (c)
- Use the appropriate box command with 9 rectangles to display a
lower sum approximation to the area under the curve. Explain your
choice of box command.
- (d)
- For n = 20,40,80, approximate the area under the curve with a
lower sum.
- (e)
- Find the smallest value of n for which the upper sum minus
the lower sum will be less than 0.005. Justify your answer by
showing that your n does work and that n - 1 does not work.
Comment as needed on your work.
- (f)
- Based on your answer in (e), give the interval in which the
actual value of the area must lie. Explain.
- 3.
- Consider h(x) = 3 + 2x - x2 on the inteval [0,3]. For
n = 60, find the upper sum and lower sum approximations to the area
under the curve. Be sure to indicate clearly which is which and to
comment on the motivation for your use of the expressions you
evaluate. (Be careful; you may want to use box commands to picture
what you are doing. Also, be careful as to how you treat the
subintervals.)
- 4.
- Consider k(x) = x3 - 2x2 - 5x + 6. We discuss the total
square units of area bounded by the graph of the function and the
x-axis on the interval [1,4].
- (a)
- For n = 60, do a midpoint rule approximation. Note that
k(3.5) = 6.875 and k(4) = 18. Explain why this suggests there
are more than 3 square units of area.
- (b)
- Note the apparent contradiction implicit in (a) and explain how
to resolve it.
- (c)
- For n = 60, find a true midpoint rule approximation to the
total square units of area.
- 5.
- Previously we have considered the area between the graph of a
function and the x-axis. Now we look at the area between two
graphs. Consider f(x) = x3 + 1 and g(x) = x2 - x + 1 on the
interval [0,1]. For n = 80, do a midpoint rule approximation to
the area between the graphs of these two functions. Discuss how you
are describing the heights of the approximating rectangles.



Next: About this document ...
Up: Labs and Projects for
Previous: Riemann Sums
Christine Marie Bonini
3/25/1999
![]()
![]()
![]()
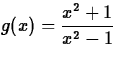 on the
interval [2,5].
on the
interval [2,5].