


Next: About this document ...
Up: Labs and Projects for
Previous: Definite Integrals
- 1.
- This exercise emphasizes that the value of a definite integral
is found as the limit of Riemann sums. Use the function g defined
in the background section.
- (a)
- Run the commands given in the background section to obtain a
right sum and find its limit.
- (b)
- Follow the pattern of the sample commands to obtain a left sum
and find its limit.
- (c)
- Follow the pattern of the sample commands to obtain a middle
point sum and find its limit.
- (d)
- What theorem in the text guarantees that the limits in (a), (b)
and (c) are the same? What property of g makes it possible to
apply that theorem here? Comment on your answer.
- 2.
- Use the int command to try to find antiderivatives for the
following functions. What important part is missing from the answers
that Maple provided?
- (a)
-
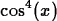
- (b)
-
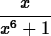
- (c)
-
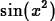
This problem shows that Maple cannot always find a ``nice''
antiderivative. The problem may not be with Maple; some functions do
not have usable antiderivatives.
- 3.
- Use the int command to try to evaluate the following
definite integrals.
- (a)
-
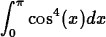
- (b)
-
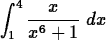
The answer is complicated looking. Use evalf to approximate it.
- (c)
-
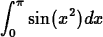
Use evalf to approximate the odd looking answer.
- 4.
- Recall that
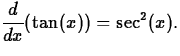
- (a)
- Consider
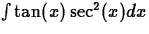 . Note that this has the form
. Note that this has the form
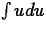 with
with 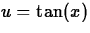 . Find the antiderivative by hand
(not by Maple).
. Find the antiderivative by hand
(not by Maple).
- (b)
- Use Maple to evaluate
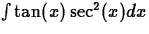 .
. - (c)
- Since the answers in (a) and (b) are not the same, who is wrong?
Can it be that both you and Maple are correct? Explain what is
happening.
- 5.
- Consider
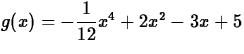 on the interval
[-1,2].
on the interval
[-1,2].
- (a)
- Use Maple to set up M6. Use evalf to evaluate the
expression Maple gives.
- (b)
- If M6 is used to approximate
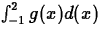 , what
accuracy is guaranteed by the error bound formula? That is, what is
the greatest amount by which M6 might differ from
, what
accuracy is guaranteed by the error bound formula? That is, what is
the greatest amount by which M6 might differ from
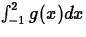 ? (This part of the exercise can be done by hand
on a sheet attached at the back of the Maple pages.)
? (This part of the exercise can be done by hand
on a sheet attached at the back of the Maple pages.)
- (c)
- Use (a) and (b) to give an interval in which the number
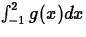 must be contained.
must be contained.
- (d)
- In fact, how good an approximation is M6? Use int to
get the exact value of
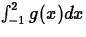 . (You should not have done
this prior to now.) Compute
. (You should not have done
this prior to now.) Compute
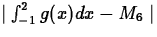 . How
does this number compare with your answer in (b)? Explain why the two
numbers differ.
. How
does this number compare with your answer in (b)? Explain why the two
numbers differ.



Next: About this document ...
Up: Labs and Projects for
Previous: Definite Integrals
Christine Marie Bonini
4/5/1999
![]()
![]()
![]()
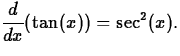
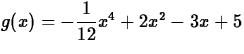 on the interval
[-1,2].
on the interval
[-1,2].