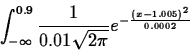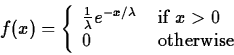Subsections

• Introduction
• Getting Started
• Background
• Exercises

Improper integrals and probability density functions

Introduction

Improper integrals like the ones we have been considering in class have many applications, for example in thermodynamics and heat transfer. In this lab we will consider the role of improper integrals in probability, which also has many applications in science and engineering.

Getting Started

To assist you, there is a worksheet associated with this lab that contains examples and even solutions to some of the exercises. You can copy that worksheet to your home directory with the following command, which must be run in a terminal window, not in Maple.

cp ~bfarr/Probability_start.mws ~

You can copy the worksheet now, but you should read through the lab before you load it into Maple. Once you have read to the exercises, start up Maple, load the worksheet Probability_start.mws, and go through it carefully. Then you can start working on the exercises.

Background

The first concept we need is that of a random variable. Intuitively, a random variable is used to measure an outcome whose value is not certain. For example, the number of hours that a hard disk can run before failing is a random variable because it is not the same for every drive, even if we only consider identical drives from the same production run. A few other examples of random variables that are important in science, engineering, or manufacturing are given below.

• The time it takes for a packet of information to travel from one location to another on the Internet.
• The number of miles that an automobile tire can be driven before it fails.
• The lengths of supposedly identical bolts manufactured by a particular production line.
• The speed of a particular gas molecule in a sample of a gas.

You may be more familiar with what are called discrete random variables, for example the number of heads obtained in ten tosses of a coin, which can only take a finite number of discrete values. In the case of a discrete random variable, the probability of a single outcome can be positive. For example, the probability that a single flip of a coin produces tails is 50%. The situation is very different when we consider a random variable like the number of miles a tire can be driven before failure, which can take any value from zero to something over $100,000$ miles. Since there are an infinite number of possible outcomes, the probability that the tire fails at exactly some number of miles, for example $50,000$ miles, is zero. However, we would expect that the probability that the tire would fail between $40,000$ miles and $100,000$ miles would not be zero, but would be a positive number.

A random variable that can take on a continuous range of values is called a continuous random variable. There turn out to be lots of applications of continuous random variables in science, engineering, and business, so a lot of effort has gone into devising mathematical models. These mathematical models are all based on the following definition.

Definition 1   We say that a random variable $X$ is continuous if there is a function $f(x)$, called the probability density function, such that

1. $f(x) \geq 0$, for all $x$
2. $\int_{- \infty}^{\infty} f(x) \, dx = 1$
3. $P(a \leq X \leq b) = \int_{a}^{b} f(x) \, dx$ where $P(a \leq X \leq b)$ represents the probability that the random variable $X$ is greater than or equal to $a$ but less than or equal to $b$.

For example, consider the following function.

$$f(x) = \left\{ \begin{array}{ll} e^{-x} & \mbox{ if $x > 0$} \\ 0 & \mbox{ otherwise} \end{array} \right.$$

This function is non-negative, and also satisfies the second condition, since

$$\int_{- \infty}^{\infty} f(x) \, dx = \int_{0}^{\infty} e^{-x} \, dx = 1$$

which is pretty easy to show. So this could be a probability density function for a continuous random variable $X$.

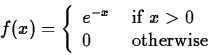
A lot of the effort involved in modeling a random process, that is, a process whose outcome is a random variable, is in finding a suitable probability density function. Over the years, lots of different functions have been proposed and used. One thing that they all have in common, though, is that they depend on parameters. For example, the general exponential probability density function is defined as

$$f(x) = \left\{ \begin{array}{ll} \frac{1}{\lambda}e^{-x/\lam... ...{ if $x > 0$} \\ 0 & \mbox{ otherwise} \end{array} \right.$$

where $\lambda$ is a positive parameter that can be adjusted to get the best fit to any particular situation.

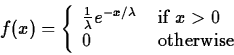
The process of deciding what probability density function to use and how to determine the parameters is very complicated and can involve very sophisticated mathematics. However, in the simple approach we are taking here, the problem of determining the parameter value(s) often depends on quantities that can be determined experimentally, for example by collecting data on tire failure. For our purposes, the two most important quantities are the mean, $\mu$ and the standard deviation $\sigma$. The mean is defined by

$$\mu = \int_{- \infty}^{\infty} x f(x) \, dx$$

and the standard deviation is the square root of the variance, $V$, which is defined by

$$V = \int_{- \infty}^{\infty} (x- \mu)^2 f(x) \, dx$$

In practice, the variance $V$ is often computed as follows,

$$V = \int_{- \infty}^{\infty} x^2 f(x) \, dx - \mu^2$$

which can be easily be obtained by expanding $(x-\mu)^2$ and writing $V$ as the sum of three integrals.

Probably the most important distribution is the normal distribution, widely referred to as the bell-shaped curve. The probability density function for a normal distribution with mean $\mu$ and standard deviation $\sigma$ is given by the following equation.

$$f(x) = \frac{1}{\sigma \sqrt{2 \pi}} e^{- \frac{(x- \mu)^2}{2 \sigma^2}} , \mbox{ for $- \infty < x < \infty$\ }$$

This distribution has a tremendous number of applications in science, engineering, and business. The exercises provide a few simple ones.

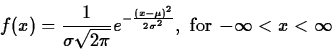
In applications, one generally has to know in advance that the random variable you want to model has, approximately, a certain kind of distribution. How one would determine this is way beyond the scope of this course, so we won't really discuss it. On the other hand, once you know, for example, that your random variable has a normal distribution you only need the values of the mean and the standard deviation to be able to model it. The exponential distribution is even simpler, since it only has one parameter, and you only need to know the mean of your random variable to use this distribution to model it.

One thing to keep in mind when you are using the normal distribution as a model is that calculations can involve values of your random variable that don't make physical sense. For example, suppose that a machining operation produces steel shafts whose diameters have a normal distribution, with a mean of $1.005$ inches and a standard deviation of $0.01$ inch. If you were asked to compute the percentage of the shafts in a certain production run had diameters less than $0.9$ inches you would use the following integral

$$\int_{- \infty}^{0.9} \frac{1}{0.01 \sqrt{2 \pi}} e^{- \frac{(x- 1.005)^2}{ 0.0002}}$$

even though negative values for the shaft diameters don't make sense.

Exercises

1. Show that the probability density function given for the exponential distribution,
   
   $$f(x) = \left\{ \begin{array}{ll} \frac{1}{\lambda}e^{-x/\lam... ...{ if $x > 0$} \\ 0 & \mbox{ otherwise} \end{array} \right.$$
   
   
   satisfies the condition
   
   $$\int_{- \infty}^{\infty} f(x) \, dx =1$$
   
   
   as long as $\lambda$ is a positive number. What would happen if $\lambda$ was negative?

2. Show that the mean and the standard deviation of the exponential distribution are both equal to $\lambda$.

3. The time (in hours) required to repair a machine is exponentially distributed with a mean $\lambda = 1/2$. What is the probability that a repair takes longer than 1 hour?

4. The systolic blood pressure of 18 year old women is normally distributed with a mean of 120 mm Hg and a standard deviation of 12 mm Hg. What is the probability that the blood pressure of a randomly selected 18 year old woman will be greater than 150 mm Hg? Between 105 and 125? (Hint - use the normal distribution function for this exercise.)

5. The time until first failure of a brand of ink jet printers is approximately normally distributed with a mean of 750 days and a standard deviation of 200 days. What fraction of these printers will fail before 1000 days?