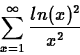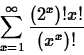Subsections

• Background
• Exercises

Sequences and Series

Background

A sequence of numbers with a specific pattern can be written in Maple as a function. This sequence can be evaluated and plotted as in the following examples.

>a1[n]:=n->3-n^(-1);
>a2[n]:=n->n;
>seq(a1[n](i),i=1..10);
>seq(a2[n](i),i=1..10);

Note that the i in the seq command is there to list the range of integers.

>plot([[k,a1[n](k)]$k=1..10],style=point);
>plot([[k,a2[n](k)]$k=1..10],style=point);

Remember to use the point style as it is a sequence and only the integers are used in the domain, i.e. don't connect the dots.

A series is a sum of the terms of a sequence.

>S1:=m->sum(a1[n](j),j=1..m);
>S2:=m->sum(a2[n](j),j=1..m);
>S1[m](1);

This is the sum of the first term.

>S1[m](2);

This is the sum of the first and second term.

>S2[m](1);
>S2[m](2);
>S2[m](3);
>S2[m](4);

The sequence of sums therefore would be:

>seq(S1[m](i),i=1..10);

Does this sequence of sums converge?

>plot([[k,S1[m](k)]$k=1..10],x=0..10,y=0..30,style=point);

Looks like it is divergent.

>seq(S2[m](i),i=1..10);

This is a sequence of sums, you can check the sequence terms from the begining of the lab to understand the sum.

>plot([[[k,S2[m](k)]$k=1..10],x=0..10,y=0..60,style=point);

It looks divergent. To check, first find the $S_{m}$ term of the sequence of sums.

>b2[n]:=n->n*(n+1)/2;

Check b2 is correctly written by comparing to the sum of sequences above.

>seq(b2[n](i),i=1..10);

This is the same output. Now that the correct function is obtained, find its limit. (Note: this function is often given to you so you don't have to examine the pattern and figure it out yourself)

>limit(b2[n](n),n=infinity);

The infinite series diverges because the limit of the sequence of partial sums diverges.

There are many tests for convergence of series. Given

$$\sum_{k=1}^n \frac{1}{\sqrt[3]{k^{4}+4}}$$

You can list its partial sums as follows

>f:=x->1/(x^4+4)^(1/3);
>Sn:=n->sum(f(i),i=1..n);
>Sn(1);Sn(2);Sn(5);
>evalf(Sn(5));
>plot([seq[k,Sn(k)],k=1..50)],style=point);

It is, however the infinite series we are concerned with. To test its convergence the integral test will be used. To use this test the function must be continuous, positive, and nonincreasing. A plot will show this.

>plot(f(x),x=1..100);

As the function satisfies the conditions, the integral test is as follows

>evalf(int(f(x),x=1..infinity);

Therefore the series is convergent.

Exercises

1. 1. Write the sequence $\frac{2n}{n+1}$ as a function.
   2. Plot the first fifteen terms.
   3. Does it appear to converge or diverge? If it seems to converge, to what does it converge?
   4. Write a function for the sum of the sequence.
   5. Plot the sequence of partial sums.
   6. Does it appear that the series converges or diverges? If it seems to converge, to what does it converge?
2. Apply the integral test to show that the given series converges.
   
   $$\sum_{x=1}^{\infty} \frac{ln(x)^2}{x^2}$$
   
   
   1. First set up the function.
   2. Plot the function. Does it seem to satisfy the necesary conditions?
   3. Take the limit of the integral. What can you concludeand why?
3. Apply the ratio test to the given series.
   
   $$\sum_{x=1}^{\infty} \frac{(2^x)!x!}{(x^x)!}$$
   
   
   1. First set up the function.
   2. Take the limit of the ratio. What do you conclude and why?