Subsections

• Introduction
• Vectors
• Exercises

Vectors

Introduction

The purpose of this lab is to acquaint you with some of the vector capabilities in Maple.

Vectors

Many commands used in this lab come from the linalg package, which must be loaded before any of the commands can be used. The following is a list of the commands discussed in this lab. Note that these form only a small subset of the package which is designed primarily for linear algebra.

$vector$

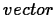
Used to define a vector.

$dotprod$

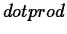
Computes the dot product of two vectors.

$crossprod$

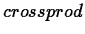
Computes the cross product of two vectors.

$evalm$

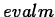
Evaluates expressions involving vectors.

$norm$

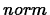
Computes the norm, or length of a vector. For reasons explained below, the use of this commmand is not recommended. A better alternative for our purposes is to use the square root of the dot product of a vector with itself.

The first set of examples below demonstrates how to compute linear combinations of vectors, dot products, lengths, and vector components for fixed vectors.

> with(linalg):
> a := [2, 13, -6];
> b := [5, -4, 17];
> a+b;
> 5*a-2*b;
> dotprod(a,b);
> crossprod(a,b);
> crossprod(b,a);
> dotprod(a,crossprod(a,b));

The next two commands show two different ways to compute the length of a vector. The first way uses the norm command. Note the 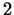$2$ as the second argument of the command. The 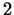$2$ has to be there, or else Maple uses a different norm than the one we want. The second way, using the fact that 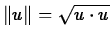$\Vert u\Vert=\sqrt{u\cdot u}$, is prefered for the reasons given in the examples below dealing with arbitrary vectors.

> norm(a,2);
> sqrt(dotprod(a,a));

The final example for fixed vectors shows two methods for computing the vector projection or component of b in the direction a. Method one first computes the unit vector of a.

> a_unit := evalm(a/sqrt(dotprod(a,a)));
> comp_a1 := evalm(dotprod(b,a_unit)*a_unit);

The second method uses the formula for the component.

> comp_a2 := evalm(dotprod(b,a)/dotprod(a,a)*a);

Exercises

1. Given the vectors $a=[9,0,-2], b=[4,-4,4], and c=[\frac{-1}{2},3,0]$ compute the following:

   a)

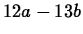
   $12a-13b$

   b)

   $7c-12(a\cdot c)b$

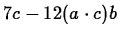
2. Given the following triangle $\bigtriangleup ABC$ with the points 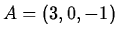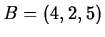$A = (3, 0, -1)$,$B = (4, 2, 5)$, and $C = (18, -2, 4)$

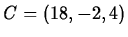
   a)

   Show that the triangle is a right triangle using the dot product.

   b)

   Find the area of the triangle using the cross product.