


Next: About this document
MA 1023 LAB 1 A'97
IMPROPER INTEGRALS and INFINITE SERIES
Before solving the exercises from today's lab, you should copy in your home-directory a MAPLE file by using the following command:
cp ~/vernescu/Mlab1.mws ~;
The file contains some examples with sequences, visualization of
sequences and series. This should complement the information and examples
that you already have in the file Maple.mws that you copied last week.
You can then start the Maple engine by using the xmaple command.
Click on FILE and OPEN Mlab1.mws. Read the examples and work some
of your own. Once you feel confortable with the commands, you can try
to solve the following exercises. You have to create your own MAPLE
file and attach a printout to your report.
- A ball has bounce coefficient 0 < r < 1 if when it is dropped from height h, it bounces back to a height of rh. Suppose that such a ball is dropped from an initial height a and subsequently bounces infinitely may times. Find the total up-and-down distance in all its bouncing. (Bonus:find the total amount of time the ball spends on bouncing given that r = 0.64 and
it is dropped from an initial height of
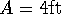 .
Assume that
.
Assume that 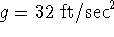 .)
.)
- Let
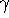 denote the graph of the function
denote the graph of the function 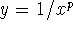 .
.
(i) Find the area of the region bounded between 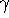 , the positive x-axis, x=1 and
, the positive x-axis, x=1 and 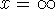 .
.
(ii) Find the volume of the solid of obtained by revolving the curve 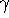 about the x-axis, between x=1 and
about the x-axis, between x=1 and 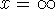 .
.
(iii) Find the area of the surface generated by revolving 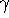 about the x-axis between x=1 and
about the x-axis between x=1 and 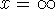 .
.
(iv) Give the range of values of p > 0 for which your answers to the above 3 problems are finite. Is there any relationship between the three quantities. (The formula for area of surface of revolution may be found on p. 400 of the text.)
- By now, it is well known that the harmonic series
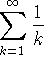 diverges. That is to say, the limit of s_n is infinite
, where
diverges. That is to say, the limit of s_n is infinite
, where 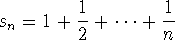 . But how fast does
. But how fast does
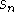 go to infinity? To answer this question, consider the sequence
go to infinity? To answer this question, consider the sequence
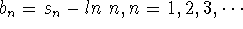 . Using maple, discover what properties this sequence have. Does it converge? If so, what does it converge to? Can you give me a rigorous reason why this sequence converges. Therefore,
. Using maple, discover what properties this sequence have. Does it converge? If so, what does it converge to? Can you give me a rigorous reason why this sequence converges. Therefore, 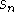 converges to infinity
like
converges to infinity
like 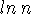 .
.
DUE:LAB TIME ON SEPTEMBER 22 OR SEPTEMBER 23.



Next: About this document
Bogdan Vernescu
Sat Sep 13 12:28:39 EDT 1997
![]() , the positive x-axis, x=1 and
, the positive x-axis, x=1 and ![]() .
.
![]() about the x-axis, between x=1 and
about the x-axis, between x=1 and ![]() .
.
![]() about the x-axis between x=1 and
about the x-axis between x=1 and ![]() .
.
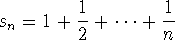 . But how fast does
. But how fast does