So far, you have considered series whose terms were constants; for example the geometric series
We can also consider series whose terms are functions. The most important such type of series is the power series
or, more generally,
The domain of f(x) is the set of x such that the series converges. This set will be an interval about x=c, called the interval of convergence. Since power series define functions, we can ask if a given function can be represented as a power series. In many cases the answer is yes. To see which power series provides the ``best fit'' to a given function F(x), we choose a point c in the domain of F. Then we require that at c, the power series and the function agree at c; and that all derivatives of the power series equal the corresponding derivatives of F(x). The result is the power series
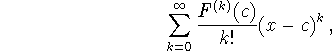
which is called the Taylor series for F(x) at c.
The Taylor series for F(x) at c is not necessarily equal to F(x) on the series's interval of convergence. (See the text, p. 555, for a counterexample.) However, if F(x) can be represented by a power series at c, the Taylor series must be the power series that does so. In practice the Taylor series does converge to the function for most functions of interest, so that the Taylor series for a function is an excellent way to work that function.
You have seen that a good strategy for working with infinite sums is to use a partial sum as an approximation, and to try to get a bound on the size of the remainder. This leads to the question of whether one can approximate a given function F(x) by using a partial sum of its Taylor series, a question which is answered by Taylor's theorem.
Theorem If f(x) and all its derivatives exist in an open interval containing c, then for each x in that interval, we may write
where
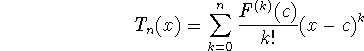
is the nth-degree Taylor polynomial of f(x) at c;
and 
, the remainder, satisfies
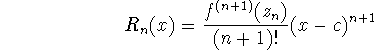
for some 
between c and x.
Observe that depends on x; hence is not a term of a Taylor
polynomial.