


Next: About this document ...
Up: lab_template
Previous: lab_template
Subsections
The purpose of this lab is to give you some experience with using the
trapezoidal rule and Simpson's rule to approximate integrals.
To assist you, there is a worksheet associated with this lab that
contains examples and even solutions to some of the exercises. You can
copy that worksheet to your home directory with the following command,
which must be run in a terminal window, not in Maple.
cp ~bfarr/NumInt_start.mws ~
You can copy the worksheet now, but you should read through the lab
before you load it into Maple. Once you have read to the exercises,
start up Maple, load
the worksheet NumInt_start.mws, and go through it
carefully. Then you can start working on the exercises.
In class we have talked about the trapezoidal rule and Simpson's rule
for approximating the definite integral
Both methods start by dividing the interval ![$[a,b]$](img2.png) into
into 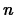 subintervals of equal length by choosing a partition
subintervals of equal length by choosing a partition
satisfying
where
is the length of each subinterval. For the trapezoidal rule, the
integral over each subinterval is approximated by the area of a
trapezoid. This gives the
following approximation to the integral
There is also an error term associated with the trapezoidal rule that
can be used to estimate the error. More precisely, we have
where
for some value 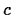 between
between 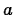 and
and 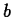 .
.
One way to use this error term is as a way to bound the number of
subintervals required to achieve a certain tolerance. That is, suppose
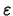 is a small number and we want to determine a value of
is a small number and we want to determine a value of
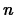 that guarantees
that guarantees
If we substitute the error formula from above into this inequality and
rearrange it to isolate 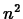 we get the following.
we get the following.
Now, if we let 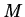 be the maximum of
be the maximum of
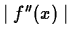 on the interval
on the interval
![$[a,b]$](img2.png) , we can take the square root of both sides of the equation to
obtain the following estimate for
, we can take the square root of both sides of the equation to
obtain the following estimate for 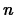 .
.
The way to think about this result is that it gives a value for 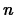 which guarantees that the error of the trapezoidal rule is less than
the tolerance
which guarantees that the error of the trapezoidal rule is less than
the tolerance 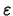 . It is generally a very conservative
result. As you will discover in the exercises, the actual number of
subintervals required to satisfy the tolerance is usually much
smaller than the number given by the error estimate.
. It is generally a very conservative
result. As you will discover in the exercises, the actual number of
subintervals required to satisfy the tolerance is usually much
smaller than the number given by the error estimate.
For Simpson's rule, the function is approximated by a parabola over
pairs of subintervals. When the areas under the parabolas are computed
and summed up, the result is the following approximation.
As for the trapezoidal rule, there is an error formula which says that
where
for some value 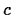 between
between 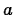 and
and 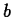 .
.
As we did for the trapezoidal rule, we can rearrange this formula to
allow us to estimate the number of subintervals required so that we
can guarantee
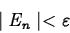
Using essentially the same steps as we used for the trapezoidal rule, we
get the following inequality.
![\begin{displaymath}n > \sqrt[4]{\frac{(b-a)^5 M}{180 \varepsilon}} \end{displaymath}](img23.png)
where 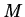 is the maximum of
is the maximum of
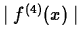 on the interval
on the interval
![$[a,b]$](img2.png) .
.
- For the following functions and intervals, complete the
following steps.
- (i)
- By using Maple's int and, possibly, evalf
commands, find a good
approximation to the integral of the function over the given interval.
- (ii)
- Use the error estimate for the trapezoidal rule to find a
value for
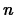 , the number of subintervals, that ensures that the error
in
, the number of subintervals, that ensures that the error
in 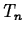 is less than
is less than 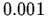 . Compute the value of
. Compute the value of 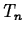 for the
value of
for the
value of 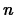 you found and verify that it is within
you found and verify that it is within 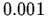 of the
value you found in part (i).
of the
value you found in part (i).
- (iii)
- Use the error estimate for Simpson's rule to find a
value for
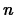 , the number of subintervals, that ensures that the error
in
, the number of subintervals, that ensures that the error
in 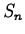 is less than
is less than 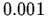 . Compute the value of
. Compute the value of 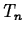 for the
value of
for the
value of 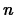 you found and verify that it is within
you found and verify that it is within 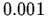 of the
value you found in part (i).
of the
value you found in part (i).
-
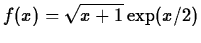 , interval
, interval ![$[0,5]$](img29.png) .
.
-
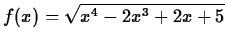 , interval
, interval ![$[-2,3]$](img31.png) .
.
- Consider the polynomial
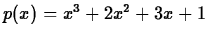 . Explain why
Simpson's rule gives the exact value of the integral
. Explain why
Simpson's rule gives the exact value of the integral
independently of the number of subintervals you use. You might want to
use the value command instead of the evalf command
on the outside of your simpson command so the result is a
fraction instead of a floating point number.



Next: About this document ...
Up: lab_template
Previous: lab_template
William W. Farr
2001-09-28
![]() is a small number and we want to determine a value of
is a small number and we want to determine a value of
![]() that guarantees
that guarantees
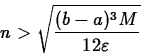
![\begin{displaymath}n > \sqrt[4]{\frac{(b-a)^5 M}{180 \varepsilon}} \end{displaymath}](img23.png)