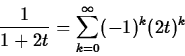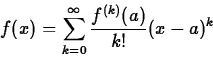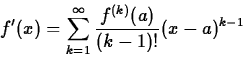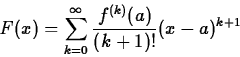Next: About this document ...
Up: lab_template
Previous: lab_template
Subsections
The purpose of this lab is to acquaint you with several useful
techniques for generating Taylor series. These techniques include
substitution and multiplication and division of series by simple
polynomials.
To assist you, there is a worksheet associated with this lab that
contains examples and even solutions to some of the exercises. You can
copy that worksheet to your home directory with the following command,
which must be run in a terminal window, not in Maple.
cp ~bfarr/Tayseries_start.mws ~
You can copy the worksheet now, but you should read through the lab
before you load it into Maple. Once you have read to the exercises,
start up Maple, load
the worksheet Tayseries_start.mws, and go through it
carefully. Then you can start working on the exercises.
The general form of the Taylor series representation with base point
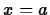 of a function
of a function 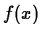 is given by the following
is given by the following
Definition 1
Suppose that
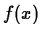
is a smooth function in some open interval
containing
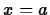
and that for every fixed value of
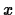
in this
interval, it can be shown that the Taylor polynomial remainder
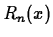
goes to zero as
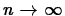
. Then the Taylor
series representation with base point
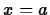
of the function
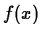
is
given by
In class you have seen the following four important Taylor series,
where the last series is really the formula for the sum of a geometric
series in disguise.
Once you have a Taylor series representation for a function, it can be used in
several ways to generate Taylor series representations of related
functions. This is because of the following theorem.
Theorem 1
Suppose
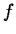
satisfies
for all
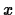
in some interval around
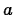
. Then,
Thus a function cannot have more than one power series in
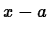
that
represents it.
The rest of the Background describes several different techniques for
generating Taylor series of functions that are related to Taylor
series that are already known. The four techniques are substitution,
multiplication and division, integration, and differentiation. We have
already seen examples of
integration and differentiation with Taylor polynomials, but we
haven't talked about the first two techniques yet.
To get a Taylor series for 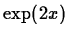 , you could go through the
standard procedure of differentiating and substituting into the
general formula, but an easier (and also correct) procedure is to take
the series for
, you could go through the
standard procedure of differentiating and substituting into the
general formula, but an easier (and also correct) procedure is to take
the series for 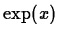 and substitute
and substitute 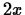 for
for 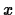 , obtaining
, obtaining
Writing out the first few terms gives
By the uniqueness theorem, this must be the Taylor series for
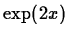 .
.
The most commonly useful Taylor series have base point 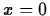 and that
is what we will focus on in this lab. The technique of substitution is
most useful if the substitution is of the form
and that
is what we will focus on in this lab. The technique of substitution is
most useful if the substitution is of the form 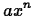 where
where 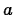 is a
constant and
is a
constant and 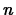 is a positive integer. For example, the series for
is a positive integer. For example, the series for
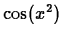 is easy to obtain as
is easy to obtain as
but it is not clear at all if the following substitution
produces a useful result. This is because you would have to do a lot
of work expanding powers of 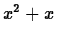 and collecting terms to recover a
power series in
and collecting terms to recover a
power series in 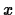 .
.
Even if you use a substitution of the form 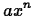 , you have to be
careful if the series is only valid for a finite interval about the
base point. For example, suppose you wanted to find the Taylor series
with base point
, you have to be
careful if the series is only valid for a finite interval about the
base point. For example, suppose you wanted to find the Taylor series
with base point 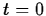 for the function
for the function
You can obtain the desired series by substitution as
but you have to be careful because this formula is not valid for all
values of 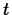 . In fact this
formula is only valid if
. In fact this
formula is only valid if
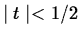 . The reason for this is
that the series for
. The reason for this is
that the series for 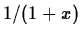 is only valid if
is only valid if
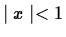 and
when we substitute
and
when we substitute 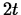 for
for 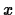 , the formula only makes sense if
, the formula only makes sense if
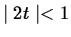 .
.
If you have the Taylor series for 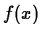 , and you want the Taylor
series for something like
, and you want the Taylor
series for something like 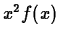 , you just multiply each term of
the series for
, you just multiply each term of
the series for 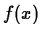 by
by 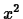 . If the leading term for the Taylor
series of
. If the leading term for the Taylor
series of 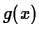 is
is 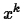 for some integer
for some integer 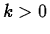 , you can use
division to obtain the Taylor series for
, you can use
division to obtain the Taylor series for 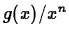 for any integer
for any integer 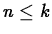 . Some examples follow.
. Some examples follow.
One of the nice properties of Taylor series is that they can be
integrated and differentiated term-by-term. Here is the formal
theorem, but the procedures are pretty straightforward.
Theorem 2
If a function
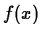
has a Taylor series representation
then the derivative of
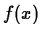
has the Taylor series representation
obtained by differentiating each term in the series for
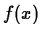
, and
the series
obtained by integrating each term in the Taylor series for
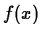
, is
an antiderivative of
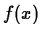
.
- Verify that substitution and multiplication work as described
above to generate Taylor series (with base point a=0) for the
following functions. That is,
compare the Taylor polynomials for various orders obtained directly
with those obtained by substitution, multiplication, or division.
-
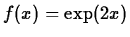 .
.
-
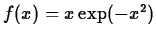 .
.
-
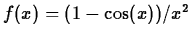 .
.
-
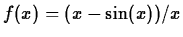 .
.
-
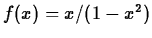 .
.
- Use substitution followed by integration to generate the first
four terms in the Taylor series with base point
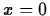 for
for
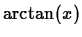 . Start with the series for
. Start with the series for 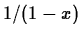 .(Hint - the
derivative of
.(Hint - the
derivative of 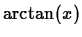 is
is 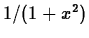 .)
.)
- In the background section we only considered multiplication of
series by polynomials. Suppose you wanted to generate the first 8
terms in the Taylor
series with base point
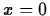 for the function
for the function
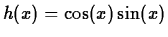 . Can you do this by multiplying Taylor
series for
. Can you do this by multiplying Taylor
series for 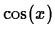 and
and 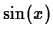 ?
?
- Compare your result in the previous exercise to the Taylor
series for
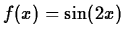 . Can you explain why it is twice your
result from the previous exercise?
. Can you explain why it is twice your
result from the previous exercise?



Next: About this document ...
Up: lab_template
Previous: lab_template
William W. Farr
2002-09-16
![]() of a function
of a function ![]() is given by the following
is given by the following
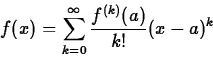
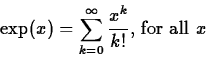
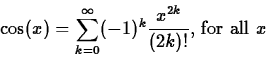
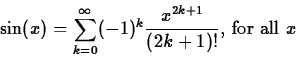
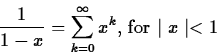
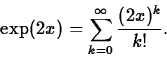
![]() and that
is what we will focus on in this lab. The technique of substitution is
most useful if the substitution is of the form
and that
is what we will focus on in this lab. The technique of substitution is
most useful if the substitution is of the form ![]() where
where ![]() is a
constant and
is a
constant and ![]() is a positive integer. For example, the series for
is a positive integer. For example, the series for
![]() is easy to obtain as
is easy to obtain as
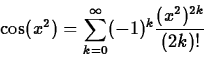
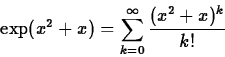
![]() , you have to be
careful if the series is only valid for a finite interval about the
base point. For example, suppose you wanted to find the Taylor series
with base point
, you have to be
careful if the series is only valid for a finite interval about the
base point. For example, suppose you wanted to find the Taylor series
with base point ![]() for the function
for the function