


Next: About this document ...
Up: lab_template
Previous: lab_template
Subsections
The purpose of this lab is to acquaint you with several useful
techniques for working with power series. These techniques include
substitution and multiplication and division of series by simple
polynomials.
To assist you, there is a worksheet associated with this lab that
contains examples and even solutions to some of the exercises. You can
copy that worksheet to your home directory with the following command,
which must be run in a terminal window, not in Maple.
cp ~bfarr/Powseries_start.mws ~
You can copy the worksheet now, but you should read through the lab
before you load it into Maple. Once you have read to the exercises,
start up Maple, load
the worksheet Powseries_start.mws, and go through it
carefully. Then you can start working on the exercises.
The general form of a power series in 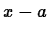 is given below.
is given below.
The number 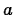 is called the base point of the power series. In this
lab, we will consider only the special case
is called the base point of the power series. In this
lab, we will consider only the special case 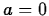 .
Historically, power series have been used most often to approximate
functions that do not have simple formulas. One example is the
exponential function, whose power series is given below, along with
another power series you have seen in class.
.
Historically, power series have been used most often to approximate
functions that do not have simple formulas. One example is the
exponential function, whose power series is given below, along with
another power series you have seen in class.
The most familiar example of a power series is the geometric series.
Another example is the power series for 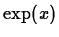 (or
(or 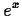 ), which is
), which is
The exercises also use the series for 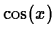 and
and 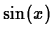 , which you
haven't seen yet, but will very soon.
, which you
haven't seen yet, but will very soon.
Once you have a convergent series representation for a function, it
can be manipulated in
several ways to generate convergent power series representations of related
functions.
The rest of the Background describes several different techniques for
generating power series representations of functions that are related to power
series that are already known. The four techniques are substitution,
multiplication and division, integration, and differentiation.
Suppose you have a power series representation for 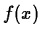 , and you
want a power series representation for
, and you
want a power series representation for 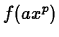 where
where 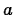 is a
constant and
is a
constant and 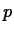 is a positive integer The theory for power series
says that you can obtain the pwer series you want simply by subsitution.
For example, to get a power series for
is a positive integer The theory for power series
says that you can obtain the pwer series you want simply by subsitution.
For example, to get a power series for 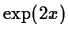 you just take
the series for
you just take
the series for 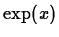 and substitute
and substitute 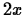 for
for 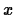 , obtaining
, obtaining
Writing out the first few terms gives
If you use such a substitution, you have to be
careful if the series is only valid for a finite interval. For
example, suppose you wanted to find the power series for
You can obtain the desired series by substitution as
but you have to be careful because this formula is not valid for all
values of 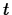 . In fact this
formula is only valid if
. In fact this
formula is only valid if
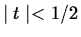 . The reason for this is
that the series for
. The reason for this is
that the series for 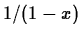 is only valid if
is only valid if
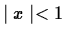 and
when we substitute
and
when we substitute 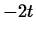 for
for 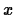 , the formula only makes sense if
, the formula only makes sense if
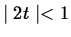 .
.
If you have a power series representation for 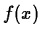 , and you want the power
series for something like
, and you want the power
series for something like 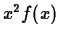 , you can just multiply each term of
the series for
, you can just multiply each term of
the series for 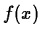 by
by 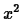 . If the leading term for the power
series representation of
. If the leading term for the power
series representation of 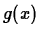 is
is 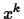 for some integer
for some integer 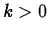 , you can use
division to obtain the power series representation for
, you can use
division to obtain the power series representation for 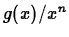 for
any integer
for
any integer 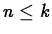 . Some examples follow.
. Some examples follow.
One of the nice properties of power series is that they can be
integrated and differentiated term-by-term. For example,
so we have the following power series representation.
Note that the interval of convergence is exactly the same as for the original
series, neglecting the behavior at the endpoints.
Integrating a power series term-by-term is very similar, but you may
have to include a constant of integration. For example, integrating
the power series representation for 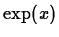 term by term gives
term by term gives
You would have to set 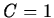 to make the right hand side the power
series representation for
to make the right hand side the power
series representation for 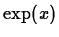 .
.
- For the
following functions,compare the partial sums of power series up to
various orders obtained directly with those obtained by applying
addition, subtraction, substitution, multiplication, or division to
the power series for
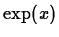 ,
, 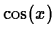 ,
, 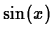 , or the geometric
series for
, or the geometric
series for 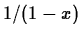 . See the examples in the Getting Started
worksheet.
. See the examples in the Getting Started
worksheet.
-
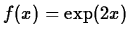 .
.
-
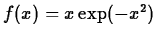 .
.
-
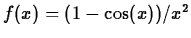
-
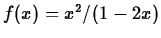 (Hint - start with the series for
(Hint - start with the series for 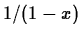 )
)
-
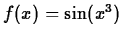
- Use substitution followed by integration to generate the first
three terms in the Taylor series with base point
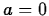 for
for
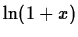 . Start with the series for
. Start with the series for 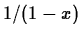 .
.
- In the background section we only considered multiplication of
series by polynomials. Suppose you wanted to generate the Taylor
polynomial of order ten with base point
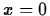 for the function
for the function
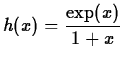 . Can you do this by
multiplying Taylor
polynomials for
. Can you do this by
multiplying Taylor
polynomials for 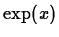 and
and
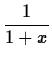 ?
?



Next: About this document ...
Up: lab_template
Previous: lab_template
William W. Farr
2003-11-14
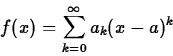
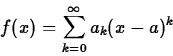
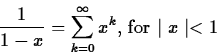
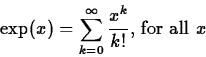
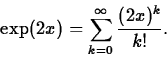
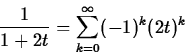
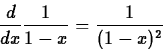
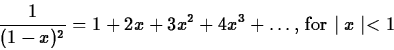
![]() term by term gives
term by term gives
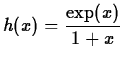 . Can you do this by
multiplying Taylor
polynomials for
. Can you do this by
multiplying Taylor
polynomials for 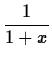 ?
?