Subsections

• Purpose
• Getting Started
• Background
• Angle between two vectors
• Vector Projection
• Area of a Triangle
• Vector Functions
• Exercises

Vector Computations and Vector Functions

Purpose

The purpose of this lab is to use Maple to introduce you to a number of useful commands for working with vectors, including some applications. The commands come from the Maple linalg and CalcP7 packages which must be loaded before any of its commands can be used.

Getting Started

To assist you, there is a worksheet associated with this lab that contains examples similar to some of the exercises. You can copy that worksheet to your home directory with the following command, which must be run in a terminal window, not in Maple.

cp /math/calclab/MA1023/Vector_start2.mws ~/My_Documents

You can copy the worksheet now, but you should read through the lab before you load it into Maple. Once you have read through the exercises, start up Maple, load the worksheet, and go through it carefully. Then you can start working on the exercises.

Background

The commands below are some of the most basic vector commands. Some examples using these commands can be found in the Getting Started Worksheet. More examples can be found in the Help screens for each command.

innerprod
Computes the dot product (also known as the inner product) of two vectors.
crossprod
Computes the cross product of two vectors.
evalm
Evaluates expressions involving vectors (and matrices).
norm
Computes the norm, or length, of a vector.

Angle between two vectors

If $\theta$ is the angle between the vectors ${\bf a}$ and ${\bf b}$, then ${\bf a} \cdot {\bf b}=\vert{\bf a}\vert\vert{\bf b}\vert \cos(\theta)$.

Vector Projection

The vector projection of ${\bf b}$ onto ${\bf a}$ or the component of ${\bf b}$ in the direction of ${\bf a}$ can be found using the following formula:

$$pr_a{\bf b} = ({\bf b} \cdot {\bf a}/\vert{\bf a}\vert^2){\bf a}$$

Area of a Triangle

The triangle created by connecting the terminal ends of the vectors ${\bf a}$ and ${\bf b}$ in standard form has area = $\frac{1}{2}\vert{\bf a} X {\bf b}\vert$.

Vector Functions

By parametric curve in the plane, we mean a pair of equations $x=f(t)$ and $y=g(t)$ for $t$ in some interval . A vector-valued function in the plane is a function ${\bf r}(t)$ that associates a vector in the plane with each value of $t$ in its domain. Such a vector valued function can always be written in component form as follows,

$${\bf r}(t) = f(t) {\bf i} + g(t) {\bf j}$$

where $f$ and $g$ are functions defined on some interval $I$. From our definition of a parametric curve, it should be clear that you can always associate a parametric curve with a vector-valued function by just considering the curve traced out by the head of the vector. The VPlot command is part of the plots package and will show the graph of the curve traced out by the terminal ends of the given vector function.

For this lab, we will assume that we have a vector-valued function ${\bf r}(t)$ that gives the position at time $t$ of a moving point $P$ in the plane. The velocity of this point is given by the derivative ${\bf r}'(t)$ and the acceleration is given by the second derivative, ${\bf r}''(t)$. In many applications of curvilinear motion, we need to know the magnitude of the velocity, or the speed. This is easy to compute - just take the magnitude $\vert{\bf r}'(t)\vert$. If you think of the speed as the rate of change of distance along the curve, and recall that arc length is distance measured along the curve, then you have the following interpretation of the speed

$$\frac{ds}{dt} = \vert{\bf r}'(t)\vert$$

where $S$ is arc length. If the speed is not zero for any value of $t$ in the interval $I$, then it is possible to define a unit vector, ${\bf T}(t)$ that is tangent to the curve as follows.

$${\bf T}(t)= \frac{{\bf r}'(t)}{\vert{\bf r}'(t)\vert}$$

Using this definition, you can write the velocity in the following form.

$${\bf r}'(t) = \frac{ds}{dt} {\bf T}(t)$$

This is not the most useful form for calculating the velocity, but it does lead to a useful way of thinking about the acceleration experience by a particle moving in a curvilinear path. If the path is a straight line, acceleration depends only on whether the particle is speeding up or slowing down. In a curve, however, there is an additional acceleration, called the centripetal acceleration, that is needed to keep the particle moving on the curve. The magnitude of this acceleration depends on the speed of the car and how much the path is curving. It turns out that you can quantify this with an intrinsic property of the curve called the curvature, usually denoted $\kappa$, defined by the following equation.

$$\kappa = \vert\frac{d{\bf T}}{ds}\vert$$

That is, the curvature is the magnitude of the rate of change of the tangent vector $T$ with respect to arc length. For example, the curvature of a straight line is zero and it can be shown that the curvature of a circle of radius $R$ is the same for every point on the circle and is given by $\kappa = 1/R$. The Maple Speed command computes the speed of a vector function and the Curvature command computes the curvature of a vector function.

Exercises

1. Given the vectors ${\bf a} = [4.238,-5,15.01]$ and ${\bf b} = [1.3,-2,-20]$, and ${\bf c} = [-\pi,2.567,0]$, use Maple to compute the numeric value of the following expressions, if possible. For those that cannot be computed because they make no sense, please explain what is wrong.

   a)

   $2{\bf a} - {\bf b}$

   b)

   $({\bf a}\cdot{\bf c})-({\bf b}\cdot{\bf c})$

   c)

   $({\bf b}\cdot{\bf b})({\bf a}X{\bf c})$

   d)

   $({\bf c}\cdot{\bf a})X{\bf b}$

2. For the three parallelograms A, B, and C whose vertices are:

   A

   
   

   $$P1=(-3,-15,-1), P2=(2-\frac{\sqrt{10}}{\sqrt{7}},-1-\frac{\sqrt{10}}{2\sqrt{7}},7+\frac{3\sqrt{10}}{2\sqrt{7}}),$$

   
   

   
   

   $$P3=(7,13,15),P4=(2+\frac{\sqrt{10}}{\sqrt{7}},-1+\frac{\sqrt{10}}{2\sqrt{7}},7-\frac{3\sqrt{10}}{2\sqrt{7}})$$

   
   

   B

   
   

   $$P1=(-1,1,1),P2=(-1,2,2),P3=(-3,5,-4),P4=(-3,4,-5)$$

   
   

   C

   
   

   $$P1(1,2,-1),P2=(4,2,-3),P3=(9,-5,0),P4=(6,-5,2)$$

   
   

   Do the following:

   i)

   Find the area of the parallelogram (Hint:Since a parallelogram is twice a triangle check out the triangle area formula)

   ii)

   The diagonals of a parallelogram are perpendicular if and only if their diagonals are perpendicular. Show whether or not the parallelogram is a rhombus.

   iii)

   Graph the parallelogram. As an example for A the plot command would be:

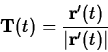
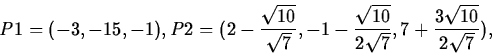
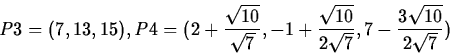
   >PLOT3D(POLYGONS([[-3,-15,-1],[0.80477,-1.597614,8.7928429],[7,13,15],
   [3.1952286,-0.40238569,5.207157]]),AXESSTYLE(NORMAL),AXESLABELS(x,y,z)
   ,VIEW(-10..10,-20..20,-1..20));
   

3. Given the box whose dimensions are $3x10x4$:

   a)

   Enter this plot command:

   >PLOT3D(POLYGONS([[0,0,0],[3,0,0],[3,10,0],[0,10,0]],
   [[0,0,0],[0,10,0],[0,10,4],[0,0,4]],[[3,0,0],[3,10,0],
   [3,10,4],[3,0,4]],[[0,0,0],[3,0,0],[3,0,4],[0,0,4]],
   [[0,10,0],[3,10,0],[3,10,4],[0,10,4]],[[0,0,4],[3,0,4],
   [3,10,4],[0,10,4]]),AXES(NORMAL), COLOR(ZHUE),
   VIEW(0..10,0..10,0..10),AXESLABELS(x,y,z));
   

   b)

   Find the volume using geometry.

   c)

   Find the volume using the vector formula for a parallelopiped:
   

   $$\vert{\bf u}\cdot({\bf v}X{\bf w})\vert$$