


Next: About this document ...
Up: lab_template
Previous: lab_template
Subsections
The purpose of this lab is to use Maple to introduce you to the notion
of improper integral and to give you practice with this concept by
using it to prove convergence or divergence of integrals involving
unbounded integrands or unbounded intervals or both.
We start with the following definition.
Definition 1
We say that the integral
is improper if
one or both of the following conditions is satisfied.
- The interval of integration is unbounded.
- The function
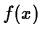 has an infinite discontinuity at some point
has an infinite discontinuity at some point
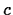 in
in ![$[a,b]$](img4.png) . That is,
. That is,
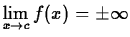 .
.
To see how to handle the problem of an unbounded integrand, we start
with the following special cases.
Definition 2
Suppose that
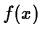
is continuous on
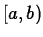
, but
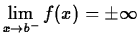
. Then we define
provided that the limit on the right-hand side exists and is finite,
in which case we say the integral converges and is equal to the value
of the limit. If the limit is infinite or doesn't exist, we say the
integral diverges or fails to exist and we cannot compute it.
Definition 3
Suppose that
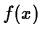
is continuous on
![$(a,b]$](img9.png)
, but
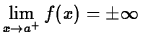
. Then we define
provided that the limit on the right-hand side exists and is finite,
in which case we say the integral converges and is equal to the value
of the limit. If the limit is infinite or doesn't exist, we say the
integral diverges or fails to exist and we cannot compute it.
Cases where 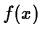 has an infinite discontinuity only at an interior
point
has an infinite discontinuity only at an interior
point 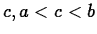 are handled by writing
are handled by writing
and using the definitions to see if the integrals on the right-hand
side exist. If both exist then the integral on the left-hand
side exists. If either of the integrals on the right-hand side
diverges, then
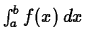 does not exist.
does not exist.
Here is a simple example using Maple to show that
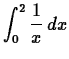 doesn't exist.
doesn't exist.
> ex1 := int(1/x,x=a..2);
> limit(ex1,a=0,right);
The example above used the right option to limit
because the right-hand limit was needed. If you need a left-hand
limit, use the left option in the limit command. Maple can usually do the limit within the int command.
> int(1/x,x=0..2);
These are handled in a similar fashion by using limits. The definition
we need the most is given below.
Definition 4
Suppose
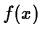
is continuous on the unbounded interval
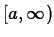
.
Then we define
provided the limit on the right-hand side exists and is finite, in
which case we say the integral converges and and is equal to the value
of the limit. If the limit is infinite or fails to exist we say the
integral diverges or fails to exist.
The other two cases are handled similarly. You are asked to provide
suitable definitions for them in one of the exercises.
Using the definition for
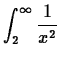 .
.
> ex2:=int(1/x^2,x=2..a);
> limit(ex2,a=infinity);
This command shows that Maple takes the limit definition into account in the int command.
> int(1/x^2,x=2..infinity);
- The gamma function is an example of an improper integral often used to approximate non-integer factorials and is defined below:
Evaluate 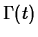 by calculating the improper integral for
by calculating the improper integral for
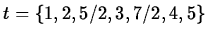 and for each integer value of
and for each integer value of 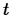 , check your answer by calculating
, check your answer by calculating 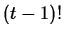 .
.
- Both of the following improper integrals given below do not exist. Show, by calculating a limit, why they do not exist.
- A
-
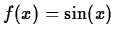 , interval
, interval 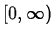 .
.
- B
-
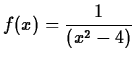 , interval
, interval ![$[-2, 2]$](img27.png) .
.
- Plot
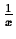 and
and 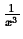 on a single graph.Recall from Calculus II that the volume of a solid of revolution formed by rotating
on a single graph.Recall from Calculus II that the volume of a solid of revolution formed by rotating 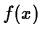 about the
about the 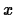 -axis over the interval
-axis over the interval ![$[a,b]$](img4.png) is
is
. Find the volume of the solid obtained by revolving the curve
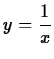 about the
about the 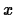 -axis, between
-axis, between 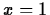 and
and 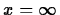 . Repeat this using
. Repeat this using
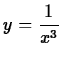 .
.



Next: About this document ...
Up: lab_template
Previous: lab_template
Jane E Bouchard
2010-10-25
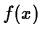 has an infinite discontinuity at some point
has an infinite discontinuity at some point
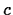 in
in ![$[a,b]$](img4.png) . That is,
. That is,
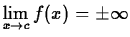 .
.
![]() has an infinite discontinuity only at an interior
point
has an infinite discontinuity only at an interior
point ![]() are handled by writing
are handled by writing
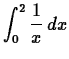 doesn't exist.
doesn't exist.
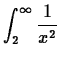 .
.
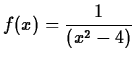 , interval
, interval 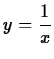 about the
about the 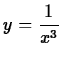 .
.