


Next: About this document ...
Up: lab_template
Previous: lab_template
Subsections
The purpose of this lab is to introduce you to curve computations
using Maple for parametric curves and vector-valued functions in the
plane.
By parametric curve in the plane, we mean a pair of equations 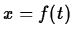 and
and 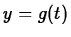 for
for 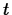 in some interval
in some interval 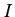 . A vector-valued function in
the plane is a function
. A vector-valued function in
the plane is a function 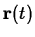 that associates a vector in
the plane with
each value of
that associates a vector in
the plane with
each value of 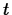 in its domain. Such a vector valued function can
always be
written in component form as follows,
in its domain. Such a vector valued function can
always be
written in component form as follows,
where 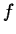 and
and 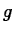 are functions defined on some interval
are functions defined on some interval 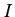 . From our
definition of a parametric curve, it should be clear that you can
always associate a
parametric curve with a vector-valued function by just considering the
curve traced out by the head of the vector.
. From our
definition of a parametric curve, it should be clear that you can
always associate a
parametric curve with a vector-valued function by just considering the
curve traced out by the head of the vector.
The easiest way to define a vector function or a parametric curve is to use the Maple list notaion with square brackets[]. Strictly speaking, this does not define something that Maple recognizes as a vector, but it will work with all of the commands you need for this lab.
>f:=t->[2*cos(t),2*sin(t)];
You can evaluate this function at any value of t in the usual way.
>f(0);
This is how to access a single component. You would use f(t)[2] to get the second component.
>f(t)[1]
The ParamPlot command is in the CalcP package so you have to load it first. If you get an error from this command, ask for help right away.
>with(CalcP7);
The ParamPlot command produces an animated plot. To see the animation, execute the command and then click on the plot region below to make the controls appear in the Context Bar just above the worksheet window.
>g:=t->[t,t^2];
>ParamPlot(g(t),t=-2..2);
You can use the VPlot command as shown below. Note that this command does not show the direction of the plot with respect to t.
>VPlot([t^2,t^3-t],t=-1.5..1.5);
The graph of a parametric curve may not have a slope at every point on
the curve. When the slope exists, it must be given by the formula
from class.
It is clear that this formula doesn't make sense if
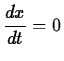 at some particular value of
at some particular value of 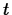 . If
. If
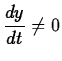 at that same value of
at that same value of 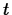 , then it turns out the
graph has a vertical tangent at that point. If both
, then it turns out the
graph has a vertical tangent at that point. If both
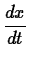 and
and
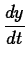 are zero at some
value of
are zero at some
value of 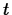 , then the curve often doesn't have a tangent line at that
point. What you see instead is a sharp corner, called a cusp.
To find the derivative of each component of the parametric equation remember to use the [ ] at the end of the command.
, then the curve often doesn't have a tangent line at that
point. What you see instead is a sharp corner, called a cusp.
To find the derivative of each component of the parametric equation remember to use the [ ] at the end of the command.
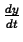 is:
is:
>diff(g(t),t)[2];
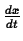 is:
is:
>diff(g(t),t)[1];
To get the derivative, divide the two:
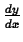 is:
is:
>m:=diff(g(t),t)[1]/diff(g(t),t)[2];
- Enter the following two parametrization as functions.
For
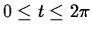 animate the two functions then animate them agaim after doubling the angles.Describe what effect doubling the angle has on the animation.
animate the two functions then animate them agaim after doubling the angles.Describe what effect doubling the angle has on the animation.
- Enter the curve
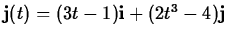
- A)
- For
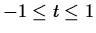 , plot the graph of
, plot the graph of 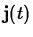 .
.
- B)
- Calculate the slope of
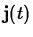 .
.
- C)
- Calculate the point at
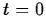 and calculate the slope at the same t.
and calculate the slope at the same t.
- D)
- Calculate the point at
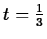 and calculate the slope at the same t.
and calculate the slope at the same t.
- Enter the parametric equation
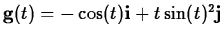 .
.
- A)
- Plot the parameterization on the domain
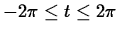
- B)
- find
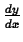
- C)
- Plot the numerator of the slope (
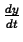 ) - use the regular plot command.Then plot the denominator of the slope (
) - use the regular plot command.Then plot the denominator of the slope (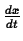 ).
).
- D)
- Keeping your work clearly organized - use fsolve commands to find where the numerator equals zero.Then find where the denominator equals zero. (The plots from part C should tell you how many solutions to look for)
- E)
- At what t-values are there horizontal tangents?
- F)
- At what t-values are there vertical tangents?
- G)
- At what t-values are there cusps?



Next: About this document ...
Up: lab_template
Previous: lab_template
Jane E Bouchard
2010-10-27
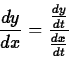
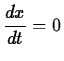 at some particular value of
at some particular value of 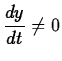 at that same value of
at that same value of