


Next: The Root Test
Up: lab_template
Previous: The Integral Test
The Ratio Test for convergence of a series can be thought of as a measurement of how fast the series is increasing or decreasing. This can be found by looking at the ratio
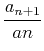 as
as
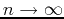 .
.
Given the series
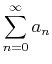 , suppose that
, suppose that
Then
- the series converges if
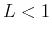 ,
,
- the series diverges if
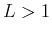 ,
,
- the test is inconclusive if
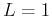 .
.
Dina J. Solitro-Rassias
2017-11-09
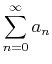 , suppose that
, suppose that
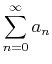 , suppose that
, suppose that