Background

In the previous lab, we introduced quadratic Taylor polynomial approximations. In this lab, we investigate higher-order Taylor polynomials.

The idea of the Taylor polynomial approximation of order n at x=a, written P_n(x,a), to a smooth function f(x) is to require that f(x) and P_n(x,a) have the same value at x=a and, furthermore, that their derivatives at x=a must match up to order n. For example the Taylor polynomial of order three for $\sin(x)$ at x=0 would have to satisfy the conditions

$$\begin{array} {ccccc} P_3(0,0) & = & \sin(0) & = & 0\ P_3'(... ...n(0) & = & 0 \ P_3'''(0,0) & = & -\cos(0) & = & -1 \end{array}$$

You should check for yourself that the cubic polynomial satisfying these four conditions is

$$P_3(x,0) = x - \frac{1}{6} x^3.$$

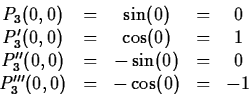
The general form of the Taylor polynomial approximation of order n to f(x) is given by the following

Theorem 494

 Suppose that f(x) is a smooth function in some open interval c ontaining x=a. Then the nth degree Taylor polynomial of the function f(x) at the point x=a is given by

We will be seeing this formula a lot, so it would be good for you to start memorizing it now! The notation f^(k)(a) is used in the definition to stand for the value of the k-th derivative of f at x=a. That is, f⁽¹⁾(a) = f'(a), f⁽³⁾(a) = f'''(a), and so on. By convention, f⁽⁰⁾(a) = f(a). Note that a is fixed and so the derivatives f^(k)(a) are just numbers. The following easier theorem should help you to see where the formula comes from.

Theorem 510

 Suppose f(x) is a smooth function in some open interval containing x=a and that k is a positive integer. Then g_k(x) defined by

$$g_k(x) = \frac{f^{(k)}(a)}{k!} (x-a)^k$$

satisfies

Maple has a command called taylor to generate these Taylor polynomial expansions, but the form it produces is not the most convenient, so two commands have been written as part of the CalcP package, which should be loaded with the following command.

  > with(CalcP):

The two procedures are called Taylor and TayPlot. The syntax for Taylor is
Taylor(f,x=a, n);,
where n is the order, f is an expression or a procedure, and a is the base point. The following examples should make the use of this procedure clear. There is also help available with the command ?Taylor.

  > Taylor(sin(x),x=0,3);

  > Taylor(sin(x),x=0,15);

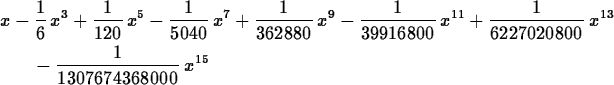
  > Taylor(sin(x),x=Pi/6,4);

  > Taylor(exp(x),x=0,5);

The result of this command is a polynomial expression that can be plotted, differentiated, etc.

It seems intuitive that the larger n is, the better the Taylor polynomial will approximate f(x). To help you investigate this, a procedure TayPlot has been written which plots f(x) and a set of Taylor polynomials simultaneously. The syntax for this command is
TayPlot(f,x=a,{n1,n2,n3, ...},x=b..d,ops);,
where f and x=a are as above, x=b..d is the usual x plot range specifier, and ops are (optional) options that TayPlot passes to the plot command. The set {n1,n2,n3, ...} consists of integers corresponding to the Taylor polynomial degrees desired. For example,

  > TayPlot(sin(x),x=0,2,3,5,x=-Pi..Pi);

  > TayPlot(sin(x),x=0,2,3,5,x=-Pi..Pi,y=-1.2..1.2);

are both valid calls of TayPlot. Both plot $\exp(x)$ and the 2nd, 3rd, and 5th order Taylor polynomial approximations. In the second TayPlot command, the y range has been set to fit the behavior of the $\sin$ function. You can plot more than three Taylor polynomials if you want, of course. You can also use a letter other than x for your independent variable. Help for TayPlot is available with the ?TayPlot command.