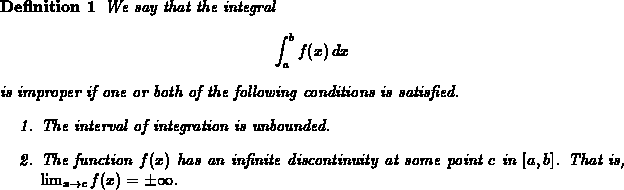Next: Unbounded integrands
Up: Improper Integrals
Previous: Purpose
Our basic theorem for 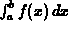 is that the integral
exists if
is that the integral
exists if 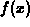 is continuous on the closed interval
is continuous on the closed interval 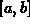 . We have
actually gone beyond this theorem a few times,
and integrated functions that were bounded
and had a finite number of jump discontinuities on
. We have
actually gone beyond this theorem a few times,
and integrated functions that were bounded
and had a finite number of jump discontinuities on 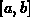 .
However, we don't have any theory to help us deal with integrals
.
However, we don't have any theory to help us deal with integrals
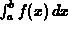 involving one or more of the following.
involving one or more of the following.
- Functions
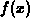 , for example rational functions, that have
vertical asymptotes in
, for example rational functions, that have
vertical asymptotes in 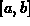 (or are not bounded on
(or are not bounded on 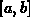 ).
).
- Integrals where the interval
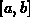 is unbounded, for example
intervals like
is unbounded, for example
intervals like 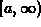 ,
, 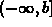 , or
, or 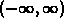 .
.
We have already seen at least one example of the problems you can run
into if the function is unbounded. Recall the clearly absurd result

that is obtained by blindly applying the FTOC. The second type of
problem, where the interval of integration is unbounded, occurs often
in applications of calculus, such as the Laplace and Fourier
transforms used to solve differential equations. It also occurs in
testing certain kinds of infinite series for convergence or
divergence, as we will learn later.
We start with the following definition.
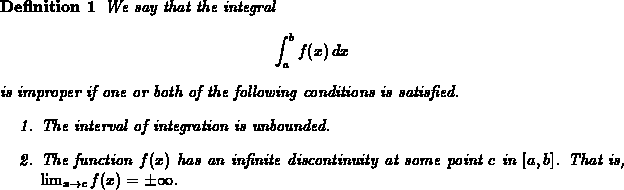
Sean O Anderson
Wed Jan 17 10:43:17 EST 1996
 is that the integral
exists if
is that the integral
exists if 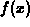 is continuous on the closed interval
is continuous on the closed interval 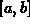 . We have
actually gone beyond this theorem a few times,
and integrated functions that were bounded
and had a finite number of jump discontinuities on
. We have
actually gone beyond this theorem a few times,
and integrated functions that were bounded
and had a finite number of jump discontinuities on 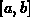 .
However, we don't have any theory to help us deal with integrals
.
However, we don't have any theory to help us deal with integrals
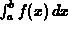 involving one or more of the following.
involving one or more of the following.
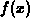 , for example rational functions, that have
vertical asymptotes in
, for example rational functions, that have
vertical asymptotes in 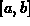 (or are not bounded on
(or are not bounded on 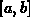 ).
).
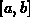 is unbounded, for example
intervals like
is unbounded, for example
intervals like 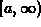 ,
, 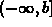 , or
, or 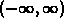 .
.