

Next: About this document
Up: Quadratic Taylor Polynomial
Previous: Background
- Use the procedure involving the solve command to find the
quadratic Taylor polynomial approximation to
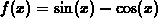 with base point
with base point 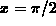 . Plot your approximation on the same graph as
. Plot your approximation on the same graph as
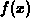 .
.
- Use the Taylor command from the CalcP package to
generate the quadratic Taylor polynomial approximation to the function
from the first exercise. Use the same base point. Verify, graphically
or otherwise, that the two quadratic polynomials are the same. You
might find the Maple expand command useful.
- Fill in the details of the proof of Theorem 1. That is, show
that the formula in the theorem satisfies the conditions in Definition
1.
- Suppose you wanted to approximate the function
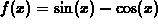 over the interval
over the interval 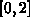 with an absolute
accuracy that is less than
with an absolute
accuracy that is less than 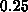 . That is, you want to choose a base
point a in this interval such that the quadratic Taylor polynomial
approximation to
. That is, you want to choose a base
point a in this interval such that the quadratic Taylor polynomial
approximation to 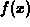 with that base point satisfies
with that base point satisfies 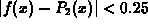 for
for 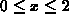 . Find a base point a that works. Include
a plot that demonstrates this.
. Find a base point a that works. Include
a plot that demonstrates this.
Sean O Anderson
Wed Jan 31 11:34:32 EST 1996
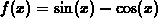 with base point
with base point 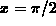 . Plot your approximation on the same graph as
. Plot your approximation on the same graph as
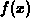 .
.
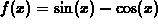 over the interval
over the interval 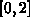 with an absolute
accuracy that is less than
with an absolute
accuracy that is less than 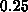 . That is, you want to choose a base
point a in this interval such that the quadratic Taylor polynomial
approximation to
. That is, you want to choose a base
point a in this interval such that the quadratic Taylor polynomial
approximation to 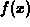 with that base point satisfies
with that base point satisfies 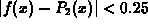 for
for 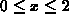 . Find a base point a that works. Include
a plot that demonstrates this.
. Find a base point a that works. Include
a plot that demonstrates this.