Summary: A one paragraph(At least 3 sentences of relevant information) summary will go here.
Exercise 1
> f:= x-> if x<1 then x^3 else -x fi;
f := proc(x) options operator,arrow; if x < 1 then x^3 else -x fi end
> f1:= x-> -x;
> f2:= x-> x^3;
> limit(f1(x), x=1,right);
> limit(f2(x), x=1,left);
> plot('f(x)', x=0..2);
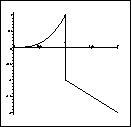
The limit of f(x) as x goes to 1 from the right is -1. The limit of f(x) as x goes to 1 from the left is 1. Since the limit from the left does not equal the limit from the right, the limit of f(x) as x goes to 1 does not exist. This is also clear in the plot above. The graph "jumps" from 1 to -1.
Exercise 2
> f:= x-> if x<0 then 5*sin(x) else x+4*sin(2*x) fi;
f := proc(x)
options operator,arrow;
if x < 0 then 5*sin(x) else x+4*sin(2*x) fi
end
> df:= D(f);
df := proc(x)
options operator,arrow;
if x < 0 then 5*cos(x) else 1+8*cos(2*x) fi
end
> limit(5*cos(x),x=0);
> limit(1+8*cos(2*x),x=0);
> plot('df(x)', x=-1..1);
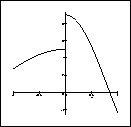
The limit as x goes to 0 from the left of f'(x) is 5. The limit as x goes to 0 from the right of f'(x) is 9. Therefore, since the limit from the left does not equal the limit from the right, the limit as x goes to 0 of f'(x) does not exist. Therefore, f(x) is not differentiable at x=0. Also, the plot above is the derivative of f(x), ( f'(x) ). It is clear that at x=0, f'(x) is not continuous. Therefore, f(x) is not differentiable at x=0.
Exercise 3
part a
> f:= x-> tan(x^2);
> D(f);
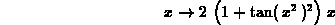
> limit((f(x+h)-f(x))/h,h=0);
The derivative of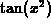 
using the D command is 
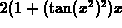which when simplified is 
.
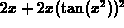The derivative of 
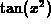using the definition of derivative is 
.
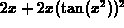As you can see, both methods produce the same correct answer.
Note: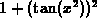 
can be written as 
.
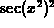part b
> f:= x-> (sin(x))^2;
> D(f);
> limit((f(x+h)-f(x))/h,h=0);
The derivative of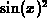 
using the D command is 
.
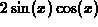The derivative of 
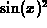using the definition of derivative is 
.
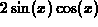As you can see, both methods produce the same correct answer.
Exercise 4
part a
> f:= x-> x^3 -(x^2+1)^(1/2) +x -3;
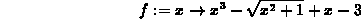
> f(1.1);
> f(1.6);
> f(1.35);
> f(1.475);
> f(1.5375);
The midpoint of [1.1,1.6] is x1=1.35. Since f(1.35) is negative, the new interval is [1.35, 1.6]. The new midpoint is x2= 1.475. Since f(1.475) is negative, the new interval is [1.475, 1.6]. The new midpoint is x3= 1.5375. Since f(1.5375) is positive, the new interval is [1.475, 1.5375]. The new midpoint is x4= 1.50625 part b
> evalf((1/(2^6)));
> evalf((1/(2^7)));
To find out how many steps are necessary to guarantee an approximation within .01 of a root, we need to use the
formula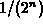 
< 0.01.
It is shown here that you need n=7 steps to be within 0.01 of a root.