next up previous
Next: About this document Up: Taylor Series Previous: Maple Commands for Taylor

Exercises

  1. For each of the following functions, give the fifth-order Taylor polynomial at the point indicated. Then plot the polynomial and the function on the same graph, using an interval of length 4 centered at the given point.
    (a)
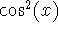    tex2html_wrap_inline180 about x=0.
    (b)
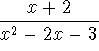    tex2html_wrap_inline184 about x=2.
    (c)
    1/x about x=1.
    (d)
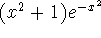    tex2html_wrap_inline192 about x=0.

  2. Plot several degrees of Taylor polynomial of tex2html_wrap_inline196 about x=0. For each, give the interval on which the polynomial is close to the function f(x). You should decide how close is ``close to f(x).'' One way to measure the interval is to plot the absolute value of the difference between the function and the Taylor polynomial.

    What happens to the interval as the degree of the polynomial gets larger? Why is it reasonable to expect that two Taylor polynomials of high degree will agree on a fairly large interval?

  3. Consider the power series tex2html_wrap_inline202 . What rational function does this power series represent? Describe what happens as larger degree Taylor polynomials are plotted against the function on the interval [0,2]. Why is the behavior different between problems 2 and 3?
  4. According to Taylor's theorem, what degree Taylor polynomial is required to estimate tex2html_wrap_inline206 to within  tex2html_wrap_inline208 on (a) the interval  tex2html_wrap_inline210 ? (b) the interval  tex2html_wrap_inline212 ?

P. Schultz
Tue Feb 4 12:52:14 EST 1997