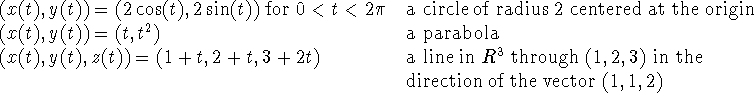
A parametrically defined curve may lie in two or three dimensions; each component (either x and y or x,y and z ) is a function of a parameter, t, which is the (only) independent variable. The set of all points (x(t), y(t)) or (x(t),y(t),z(t)) is plotted in two or three dimensions.
Some simple examples are:
Maple commands for plotting parametric functions are quite easy to use:
> plot([2*cos(t), 2*sin(t), t = 0..2*Pi]);
for a 2 dimensional curve (note where the brackets are), and
> with(plots); > spacecurve([ sin(4*t), cos(4*t), t^2, t=0..10]);
for a three dimensional curve. Please try each of these out.
When the curves are plotted by Maple, no axes will appear. The pull down menu axes allows you to put them in. Additionally, you may rotate them to a position of your choice by dragging the box that appears with the mouse; when done, click the middle mouse button and the curve will be redrawn with the new axes. Try this out on the 3d plot you just did! If the graph is too``ragged" in appearance, it is not based upon enough points. This can be adjusted by adding an option of the form numpoints = in plot or spacecurve. For example,
> spacecurve([sin(4*t), cos(4*t), t^2, t=0..10,numpoints=500]);
may improve the appearance of that 3 dimensional curve. For more information, see ?plot or ?spacecurve in Maple.
The goal of the exercises is to investigate the general shape associated with certain equations in two and three dimensions. This may be done by varying certain constants within the equations (actually called ``parameters" themselves). Maple is an excellent environment to do this in; once the command works correctly to plot an equation, one may easily change the constants and observe the changes that go along with them, with minimal effort.