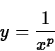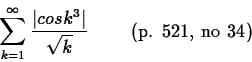

Next: About this document ...
MA 1023 LAB 1 C'98
IMPROPER INTEGRALS, SEQUENCES AND GEOMETRIC SERIES
The following maple commands may be helpful to you in doing this lab.
I shall use the function
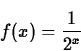
as an example.
- 1.
- To define a function, use
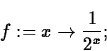
- 2.
- To integrate a function, use
int(f(x),x=1..infinity);
- 3.
- To find the sum of a finite series
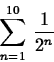
,
use
sum(f(i),i=1..n) ;
where f(x) is define above;
- 4.
- Recall that an infinite series is defined as the limit of
the sequence of partial sums. To evaluate
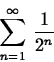
, we can define the sequence of
partial sums as a function of n by
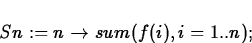
and then take the limit of Sn by using the limit command
limit(Sn(n),n=infinity);
Exercises
- 1.
- Recall from Calculus II how to compute the volume of solid of revolution.
Using
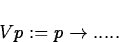
in Maple, define a function that
represents the volume of the solid of revolution
obtained by revolving the curve
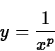
about the x-axis, between x=1 and
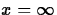 . For what values of p will this volume be finite ?
(Your answer should be an interval which may be unbounded.)
. For what values of p will this volume be finite ?
(Your answer should be an interval which may be unbounded.)
- 2.
- Repeat the above problem but this time find the surface area of the
solid of revolution. The formula for surface area is given on page 400
of the text. Is your answer the same as above ?
Is it possible for a solid to have finite volume but infinite surface area?
Is it possible for a solid to have finite surface area but infinite volume?
(The last question may not have an easy answer. Make a conjecture and
give some examples to support your case.)
- 3.
- A ball has bounce coefficient 0 < r < 1 if when it is dropped from
height h, it bounces back to a height of rh. Suppose that such a ball
is dropped from an initial height a and subsequently bounces infinitely
may times. Find the total up-and-down distance in all its bouncing.
- 4.
- I ran across the following problem while teaching Calculus
III A term which I don't know how to solve:
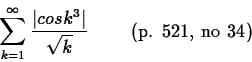
Will you help me out by forming the sequence of partial sums and finding
the limit by using finite sums? Now repeat the problem without the
absolute value in the infinite series. Does the series converge ?
(Your Lab Instructors know some secret command that will allow you to see
the graph of a sequence.)
DUE:LAB TIME ON JANUARY 21 OR 22


Next: About this document ...
Christine M Palmer
1/13/1998
![]()
![]()
![]()
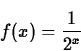
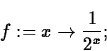
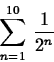
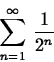
![]()
![]()