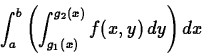Next: About this document ...
Up: lab_template
Previous: lab_template
Subsections
The purpose of this lab is to acquaint you with using Maple to do
double integrals.
To assist you, there is a worksheet associated with this lab that
contains examples. You can
copy that worksheet to your home directory with the following command,
which must be run in a terminal window, not in Maple.
cp ~bfarr/Doubleint_start.mws ~
You can copy the worksheet now, but you should read through the lab
before you load it into Maple. Once you have read to the exercises,
start up Maple, load
the worksheet Doubleint_start.mws, and go through it
carefully. Then you can start working on the exercises.
Suppose that 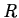 is a rectangular region in the the
is a rectangular region in the the 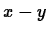 plane, and
that
plane, and
that 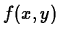 is a continuous, non-negative function on
is a continuous, non-negative function on 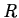 . Then the
volume of the solid above
. Then the
volume of the solid above 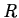 and below
and below 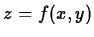 is given by the
double integral
is given by the
double integral
You learned in class that such integrals can be evaluated by either of
the iterated integrals
or
where the rectangle 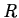 is defined by the inequalities
is defined by the inequalities
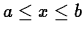 and
and
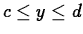 .
.
The worksheet associated with this lab contains examples of how to use
Maple to compute double integrals. It also has an example of how to
use Maple if the region of integration is of the more complicated form
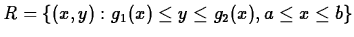 .
This is the case where the base of the solid is not rectangular, but
is bounded by two curves
.
This is the case where the base of the solid is not rectangular, but
is bounded by two curves 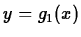 and
and 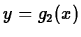 . If
. If 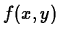 is as
before, then the volume of the solid above
is as
before, then the volume of the solid above 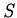 and below
and below 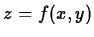 is
given by
is
given by
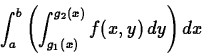
The other case, where the region 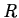 is
is 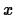 -simple can also be handled
using Maple, and there is an example in the worksheet.
-simple can also be handled
using Maple, and there is an example in the worksheet.
- Use Maple to compute the following double integrals.
-
-
-
-
- Let
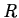 be the region in the
be the region in the 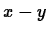 plane containing the origin and
bounded by the two curves
plane containing the origin and
bounded by the two curves
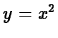 and
and 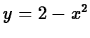 . Compute
. Compute
where
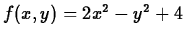 . Include a plot of the region
. Include a plot of the region 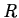 in your
worksheet.
in your
worksheet.
- Consider the following integral
where the region 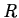 is bounded by
is bounded by 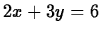 ,
, 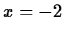 , and
, and
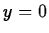 . First, plot the region
. First, plot the region 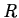 . Then
compute the integral using
. Then
compute the integral using 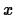 as the inner variable of integration.
Repeat the calculuation using
as the inner variable of integration.
Repeat the calculuation using 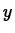 as the inner variable of
integration. You should get the same answer.
as the inner variable of
integration. You should get the same answer.
- Use a double integral to find the volume of the region beneath
the plane with equation
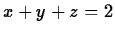 and above the triangle with
vertices
and above the triangle with
vertices 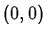 ,
, 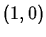 , and
, and 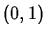 . Include a plot of the region
in the
. Include a plot of the region
in the 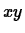 plane.
plane.



Next: About this document ...
Up: lab_template
Previous: lab_template
William W. Farr
2002-09-20
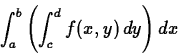
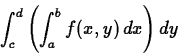
![]() .
This is the case where the base of the solid is not rectangular, but
is bounded by two curves
.
This is the case where the base of the solid is not rectangular, but
is bounded by two curves ![]() and
and ![]() . If
. If ![]() is as
before, then the volume of the solid above
is as
before, then the volume of the solid above ![]() and below
and below ![]() is
given by
is
given by