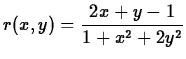The purpose of this lab is to acquaint you with techniques for finding and classifying local and global extreme values of functions of two variables.
cp ~bfarr/Extrema2D_start.mws ~
You can copy the worksheet now, but you should read through the lab before you load it into Maple. Once you have read to the exercises, start up Maple, load the worksheet Extrema2D_start.mws, and go through it carefully. Then you can start working on the exercises.
A crucial first step in solving such problems is being able to find
and classify local extreme values of a function. What we mean by a
function ![]() having a local extreme value at a point
having a local extreme value at a point ![]() is
that for values of
is
that for values of ![]() near
near ![]() ,
,
![]() for a local maximum and
for a local maximum and
![]() for a local minimum.
for a local minimum.
In single-variable
calculus, we found that we could locate candidates for local extreme
values by finding points where the first derivative vanishes. For
functions of two dimensions, the condition is that both first order
partial derivatives must vanish at a local extreme value candidate
point. Such a point is called a stationary point. It is also one of
the three types of points called critical points.
Note carefully that the condition does not say that a point where the partial
derivatives vanish must be a local extreme point. Rather, it says that
stationary points are candidates for local extrema. Just as was the case
for functions of a single variable, there can be stationary points that
are not extrema. For example, the saddle surface
![]() has a critical point at the origin, but it is not a local extremum.
has a critical point at the origin, but it is not a local extremum.
Finding and classifying the local extreme values of a function
![]() requires several steps. First, the partial derivatives must
be computed. Then the critical points must be solved for, which is not
always a simple task. Finally, each critical point must be classified
as a local maximum, local minimum, or neither. The examples in the
Getting Started worksheet
are intended to help you learn how to use Maple to simplify these tasks.
requires several steps. First, the partial derivatives must
be computed. Then the critical points must be solved for, which is not
always a simple task. Finally, each critical point must be classified
as a local maximum, local minimum, or neither. The examples in the
Getting Started worksheet
are intended to help you learn how to use Maple to simplify these tasks.