MA1024
CALCULUS IV A03 A
Gradients and Surfaces
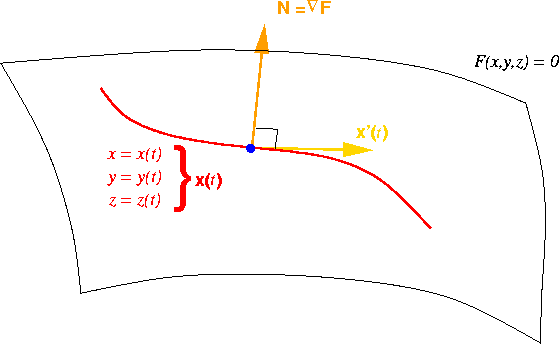
Why is Grad(F) Perpendicular
to the Surface F(x, y, z) = 0 ?
Suppose that F(x, y, z) = 0 is a smooth surface,
suppose the point
(xo, yo, zo)
lies on the surface,
and suppose that x = x(t),
y = y(t),
z = z(t) is a parameterization for an arbitrary curve
passing through
(xo, yo, zo)
at t = to.
So F(x(t), y(t), z(t)) = 0
for all t.
Applying the chain rule,
one finds that
Fxx'(t) +
Fyy'(t) +
Fzz'(t) = 0
or
Grad(F)(xo, yo, zo)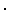 x'(to) = 0
x'(to) = 0
which implies that Grad(F) is perpendicular to x'.
Since x' is tangent to the curve,
and since this is an arbitary curve in the surface,
Grad(F) must be perpendicular to the surface.
Written by:
JDF
(E-Mail: bach@wpi.edu)
Last Updated: Friday, 19 September 2003
Copyright 2003, Joseph D. Fehribach
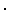 x'(to) = 0
x'(to) = 0 