The first set of examples below demonstrates how to compute linear combinations of vectors, dot and cross products, lengths, and vector components for fixed vectors.
> with(linalg):
Warning, the protected names norm and trace have been redefined and unprotected
> a := [2,13,-6];
> b := [5,-4,17];
> a+b;
> 5*a-2*b;
> innerprod(a,b);
> crossprod(a,b);
> crossprod(b,a);
Think about why the following is exactly zero:
> innerprod(a,crossprod(a,b));
The next two commands show two different ways to compute the length
of a vector. The first way uses the norm
command. Note the 2 as the second argument of the command. This
2 has to be there, or else Maple uses a different norm
than the one we want. The second way, using the fact that
|| u || = 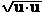 ,
is preferred for reasons given in the examples below
dealing with arbitrary vectors.
,
is preferred for reasons given in the examples below
dealing with arbitrary vectors.
> norm(a,2);
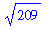
> sqrt(innerprod(a,a));
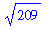
In the next set of examples, two arbitrary three-dimensional vectors, u and v, are defined and then these vectors are used to establish the vector identity
 (u - v)
= u
(u - v)
= u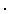 u
- 2 u
u
- 2 u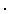 v
+ v
v
+ v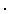 v .
v .
Note that when defining an arbitrary vector, that is, a vector whose
components are all variables, you only have to give the dimension of
the vector to the vector command.
For example, to define a four-dimensional arbitrary vector called w
the command would be w:= vector(4);.
> u := vector(3);
> v := vector(3);
The next two commands show the two ways of computing the length of an arbitrary vector. Note the absolute value signs appearing in the output of the norm command. These appear because Maple is allowing the components of u to be complex numbers. The problem is that there is not a simple way to tell Maple that the components of u are real numbers. Absolute value signs cause problems in proving vector identities involving real vectors, so you probably are better off using the square root of the dot product of a vector with itself to compute the length.
> norm(u,2);
.gif)
> sqrt(innerprod(u,u));
).gif)
The next few commands show how to prove the vector identity given above. The strategy is to compute both sides of the equation and then compare them. If they are identical, then the equation holds.
> eq1 := innerprod(evalm(u-v),evalm(u-v));
> eq2 := innerprod(u,u)+innerprod(v,v)-2*innerprod(u,v);
> simplify(eq1-eq2);
In the above lines,
the use of evalm
and simplify
is optional;
the same results would be found if these commands were left out.
In some cases, however, these sorts of clarifying commands are required
for Maple to obtain the correct answers.
Written by:
JDF
(E-Mail: bach@wpi.edu)
Last modified: Monday, 18 August 2003
Copyright 2003, Joseph D. Fehribach