


Next: About this document ...
Up: lab_template2
Previous: lab_template2
Subsections
Defining surfaces with rectangular coordinates often times becomes more complicated than necessary. A change in coordinates can simplify things. The easiest examples are a sphere and a cylinder.
> with(plots):
> f1:=x^2+y^2+z^2=49;
> g1:=rho=7;
> implicitplot3d(f1,x=-7..7,y=-7..7,z=-7..7,axes=boxed,scaling=constrained);
> implicitplot3d(g1,rho=0..7.5,theta=0..2*Pi,phi=0..Pi,coords=spherical,
numpoints=5000,axes=boxed);
> f2:=x^2+y^2=49;
> h2:=r=7;
> implicitplot3d(f2,x=-7..7,y=-7..7,z=-8..8,axes=boxed);
> implicitplot3d(h2,r=0..7.5,theta=0..2*Pi,z=-8..8,coords=cylindrical,
numpoints=3000,axes=boxed);
To change to cylindrical coordinates from rectangular coordinates use the conversion:
Where 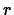 is the radius in the x-y plane and
is the radius in the x-y plane and 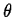 is the angle in the x-y plane.
To change to spherical coordinates from rectangular coordinates use the conversion:
is the angle in the x-y plane.
To change to spherical coordinates from rectangular coordinates use the conversion:
Where 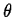 is the angle in the x-y plane;
is the angle in the x-y plane; 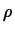 is the radius from the origin in any direction; and
is the radius from the origin in any direction; and 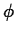 is the angle in the x-z plane.
As an example, the equation of an ellipsoid in rectangular coordinates is
is the angle in the x-z plane.
As an example, the equation of an ellipsoid in rectangular coordinates is
> f3:=x^2/23+y^2/23+z^2/122=1;
>implicitplot3d(f3,x=-5..5,y=-5..5,z=-12..12,scaling=constrained,axes=boxed);
Changing to sherical coordinates:
> g3:=simplify(subs({x=rho*sin(phi)*cos(theta),y=rho*sin(phi)*sin(theta),
z=rho*cos(phi)},f3));
> implicitplot3d(g3,rho=0..12,theta=0..2*Pi,phi=0..Pi,coords=spherical,axes=boxed,
scaling=constrained,numpoints=2000);
- Given the rectangular equation for a hyperboloid of one sheet:
- A)
- Graph the equation using the domain values of
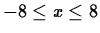 ,
,
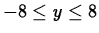 and the range values
and the range values
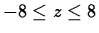 .
.
- B)
- Write the equation in spherical coordinates and then graph the equation.
- C)
- Write the equation in cylindrical coordinates and graph it.
- D)
- Looking at the three equations, which coordinates appears to give the simplest equation?
- A sphere centered at the origin (as seen in the background) is a very simple equation in spherical coordinates. Now let's look at a sphere moved away from the origin.
- A)
- Graph the equation using the domain values
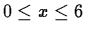 ,
,
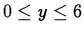 and the range values
and the range values
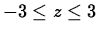 .
.
- B)
- Write the equation in spherical coordinates and graph it. (You may want to use axes=normal instead of boxed)
- C)
- Write the equation in cylindrical coordinates and graph it. (You may want to use axes=normal instead of boxed)
- D)
- Looking at the three equations, which coordinates appear to give the simplest equation?
- E)
- Looking at the rectangular domain values, a hemisphere can be graphed two ways. Changing the
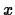 values to
values to 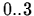 (or
(or 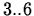 ). The second way would be to change the y values to
). The second way would be to change the y values to 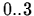 . Graph a hemisphere four ways:
. Graph a hemisphere four ways:
- i.
- In spherical coordinates change the
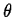 values.
values.
- ii.
- In spherical coordinates change the
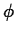 values.
values.
- iii.
- In cylindrical coordinates change the
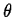 values.
values.
- iv.
- In cylindrical coordinates change the
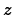 values.
values.



Next: About this document ...
Up: lab_template2
Previous: lab_template2
Jane E Bouchard
2008-10-01