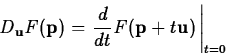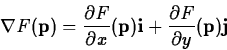Next: About this document ...
Up: lab_template
Previous: lab_template
Subsections
To assist you, there is a worksheet associated with this lab that
contains examples. You can copy the worksheet to your home directory with the following command, which must be run in a terminal window, not Maple. Go to the Start menu on the computer. In the bottom search rectangle type putty and open the putty terminal. Log in to putty as you usually log in. then copy and paste the following command:
cp /math/calclab/MA1024/Pardiff_grad_start.mws My_Documents
Now it is in your file. Open Maple and open the worksheet. Read the lab on the internet then go through the worksheet, hitting enter to see what the commands do.
For functions of two variables in Cartesian
coordinates, the graph is a set of points  in
three-dimensional space. For this reason, visualizing
functions of two variables is usually more difficult. The idea is that a plane
in
three-dimensional space. For this reason, visualizing
functions of two variables is usually more difficult. The idea is that a plane  intersects the
surface in a curve. The projection of this curve on the
intersects the
surface in a curve. The projection of this curve on the 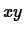 plane
is
called a level curve. A collection of such curves for different values
of
plane
is
called a level curve. A collection of such curves for different values
of 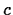 is a representation of the surface called a contour plot.
is a representation of the surface called a contour plot.
The partial derivatives
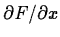 and
and
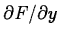 of
of 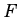 can be thought of as the rate of change of
can be thought of as the rate of change of 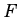 in
the direction parallel to the
in
the direction parallel to the 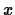 and
and 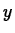 axes, respectively. The
directional derivative
axes, respectively. The
directional derivative
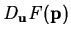 , where
, where
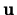 is a unit vector, is the rate of change of
is a unit vector, is the rate of change of 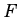 in the
direction
in the
direction 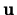 . There are several different ways that the
directional derivative can be computed. The method most often used
for hand calculation relies on the gradient, which will be described
below. It is also possible to simply use the definition
. There are several different ways that the
directional derivative can be computed. The method most often used
for hand calculation relies on the gradient, which will be described
below. It is also possible to simply use the definition
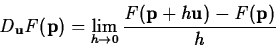
to compute the directional derivative. However, the following
computation, based on the definition, is often simpler to use.
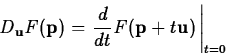
One way to think about this that can be helpful in understanding
directional derivatives is to realize that
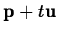 is
a straight line in the
is
a straight line in the  plane. The plane perpendicular to the
plane. The plane perpendicular to the
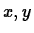 plane that contains this straight line intersects the surface
plane that contains this straight line intersects the surface 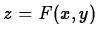 in a curve whose
in a curve whose 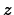 coordinate is
coordinate is
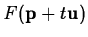 . The derivative of
. The derivative of
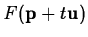 at
at 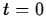 is the rate of change of
is the rate of change of 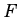 at
the point
at
the point 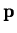 moving in the direction
moving in the direction 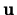 .
.
The gradient of 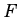 , written
, written 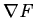 , is most easily computed as
, is most easily computed as
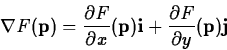
As described in the text, the gradient has several important
properties, including the following.
- Consider the following function.
First, plot the graph of this function over the domain
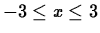 and
and
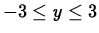 using the plot3d
command. Then use the
contourplot command to generate a contour plot of
using the plot3d
command. Then use the
contourplot command to generate a contour plot of 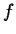 over the same domain having 22 contour lines.
over the same domain having 22 contour lines.
- Consider again the function
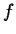 from the first exercise. Using
either method from the Getting Started worksheet, compute the
directional derivative of
from the first exercise. Using
either method from the Getting Started worksheet, compute the
directional derivative of 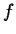 at the point
at the point 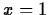 ,
, 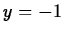 in the
three directions below.
in the
three directions below.
- A)
-
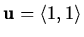
- B)
-
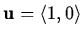
- C)
-
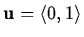
- Using the method from the Getting Started worksheet,
plot the gradient field and the contours of
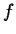 on the same plot. Use
the domain of
on the same plot. Use
the domain of
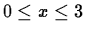 and
and
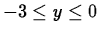 . Use 20 contours and a 20 by 20 gradient field. Can you
use this plot to explain the values for the directional derivatives
you obtained in the previous exercises? By explaining the values, I
only mean can you explain what kind of surface it is and why the values were positive, negative, or zero in terms of the contours and the gradient field?
. Use 20 contours and a 20 by 20 gradient field. Can you
use this plot to explain the values for the directional derivatives
you obtained in the previous exercises? By explaining the values, I
only mean can you explain what kind of surface it is and why the values were positive, negative, or zero in terms of the contours and the gradient field?



Next: About this document ...
Up: lab_template
Previous: lab_template
Jane E Bouchard
2010-09-20