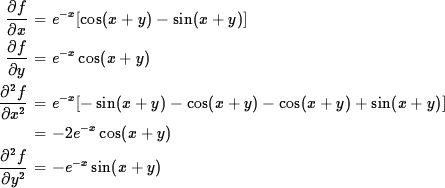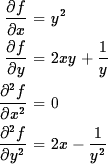1. (20 pts) Find the length of the portion of the helix
   r(t) = (4 cos t)i + (4 sin t)j + 3tk

   corresponding to the interval 0 t /2.

   Solution Arc length =

   
   
   
   
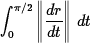
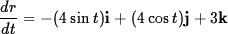
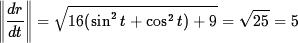
   Arc length =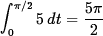

   ---

   (20 pts) Can anything be said about the speed of a particle whose acceleration is always orthogonal to its velocity? Give reasons for your answer.

   Solution The particle has velocity V and acceleration A given by

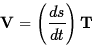     and   .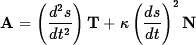

   
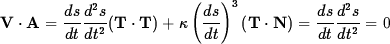
   This implies ds/dt = 0 or d²s/dt² = 0. Setting aside the case ds/dt = 0 as trivial (the particle is not moving), we conclude that d²s/dt² = 0, i.e. ds/dt = const (the speed is constant).

   ---

   (20 pts) Show that the function has no limit as (x, y) approaches (0, 0).

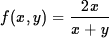
   Solution As the point (x, y) approaches (0, 0) along y=kx, then

   

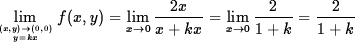
   This limit depends on k and therefore the function has no limit at the origin.

   ---

   (20 pts) Find 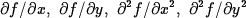for

   1. f = e^-x sin (x + y)

   2. f = 1 + xy² + ln y

   Solution

   1. 

   2. 

   ---

   (20 pts) Find the directions in which the function

   

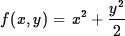
   1. increases most rapidly at the point (1, 1);

   2. decreases most rapidly at the point (1, 1).

   What is the direction of the level curve

   f(x, y) = const = f(1, 1)

   at this point?

   Solution

   

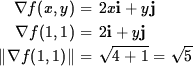
   1. The most rapid increase occurs along the vector v
      

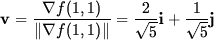
   2. The most rapid decrease occurs along the vector -v
      

   The level curve has the direction

   

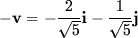
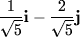
   perpendicular to v.

Back to the top