Projects

The trajectory of light as an example of the shortest path

The minimal problem
Light is known to propagate along straight lines in a uniform medium. Going from one point to another, it chooses the shortest path. In this lab, you will answer the question: What is the trajectory of light that starts at point P and passes through point Q after being reflected at some unknown point R on mirror M in between?

To specify the point R, we apply the principle of the shortest distance. This principle requires that the sum

PR + RQ be minimal. This minimum requirement alone will specify the location of R on the mirror.

First solution

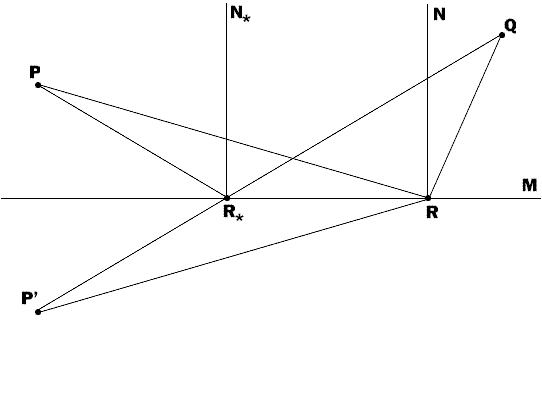
We know from daily experience that an observer at Q sees the reflected light coming from an imiginary reflected source P' seemingly located behind the mirror. The trajectory of light connecting P' with Q should be the shortest possible path between these points, i.e. it should be the straight line P'Q. This line intersects with the mirror M at point R_*. Since PR_* = P'R_*, we have PR_* + R_*Q = P'R_* + R_*Q = P'Q. This is the shortest distance because P'Q is a straight line. To prove this, assume the contrary, i.e. that the reflection occurs at some point R rather than at R_*. For the triangle P'QR we have the inequality P'R + RQ > P'Q = P'R_* + R_*Q. This inequality shows that the straight line P'Q yields the shortest possible distance.

An elementary geometric analysis shows that if N_*R_* is the normal to M at R_*, then the angle of incidence PR_*N_* is equal to the angle of the reflection N_*R_*Q

PR_*N_* =

N_*R_*Q, and this equality of angles fixes the choice R_* of R. For any other point R on the mirror, the equality of the relevant angles will not occur

PRN

NRQ.

Second solution

Introduce the function

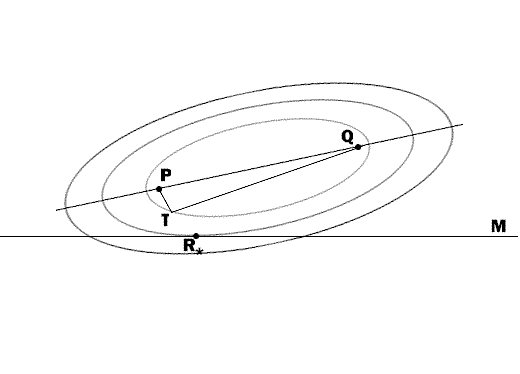
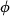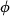(T) = PT + TQ defined as the sum of distances from two fixed points P and Q to a variable point T. Let us fix a positive number d > PQ and consider the locus of points T having the same value of

(T) equal to d:

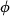(T) = d.

All such points belong to an ellipse with foci P and Q. If we choose a number d₁ > d, then the equation 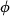(T) = d₁ will define a larger ellipse, confocal with the previous one. If we picked other values of d and plotted the corresponding ellipses, we would come up with a series of level curves 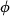(T) = const; this chart being a family of confocal ellipses with focal points P and Q.

Some of these ellipses intersect with the mirror M at two points, some do not intersect it at all, and only one ellipse has one common point with the mirror. This selected point is the required point R_* of reflection, and the relevant ellipse specifies the minimum distance PR_* + R_*Q.

Problems

Let (x_P, y_P) be the coordinates of P, (x_Q, y_Q) be the coordinates of Q, and (x, y) be the coordinates of R. Without lack of generality, we may assume that the mirror lies along the x-axis (y = 0). The sum PR + RQ can be computed PR + RQ = sqrt((x_P - x)² + y_P²) + sqrt((x_Q - x)² + y_Q²). This sum (which is a function of x) should be minimal. Let x_* be the value of x minimizing this sum and R_*(x_*, 0) be the corresponding point on the mirror.
Show by direct calculation that

min(PR + RQ) = (PR + RQ)_{x = x_*}

= PR_* + R_*Q

= P'R_* + R_*Q = P'Q

= sqrt((x_Q - x_P)² + (y_Q + y_P)²)
Comparing the first and second solutions, demonstrate the following property of an ellipse: Two straight lines connecting the focal points of an ellipse with an arbitrary point R on its periphery make equal angles with the tangent to the ellipse at point R. Your solution does not need to contain any formulas. A well-worded description will suffice.
Based on the second solution, suggest, in words, a procedure for finding the point of light reflection from a curvilinear mirror of arbitrary shape.
Three towns A, B, and C want to build three roads towards a common transportation center. They want to choose the location R of this center so as to minimize the total length of the roads and, hence, the construction costs. Formulate this minima problem and solve it by applying a procedure similar to the one described above in the second solution. Use the result of Problem 2 to give a complete descriptive characterization of the desired location R.

Back to the top

Created by Henry Fink
Last updated: Sunday, September 28, 1997