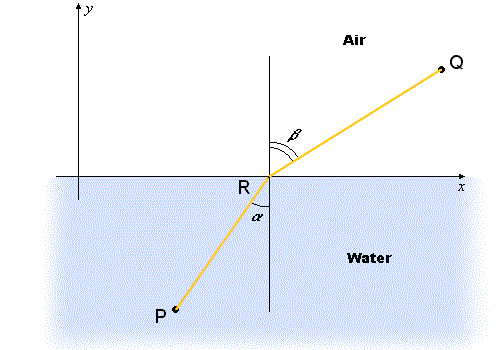
Figure 1: Refraction of light

The French mathematician Pierre de Fermat instead suggested another principle called the principle of least time. Fermat conjectured that of all the paths that light might choose to get from one point to another, it always chooses the path which takes the least amount of time. This principle is more general since it equally applies to both uniform and non-uniform media. Various media differ by the velocity at which light propagates through them. For example, in water, the velocity of light equals c_W = 225,056 km/sec while in the air it equals c_A = 291,262 km/sec. Remembering the formula rate^.time = distance, according to Fermat's Principle, light will choose the path that minimizes the quantity

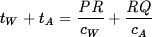(1)

which is the sum of the two times. If c_W = c_A = c (i.e. the medium is uniform), then

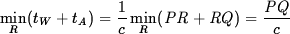
which shows that the path is a straight line as we would expect.

Getting back to Eq. 1, we can assign coordinates (x_P, y_P) to P and (x_Q, y_Q) to Q. The expression can then be written as

Problem 1
Show that the position R_*(x_*, 0) of the point of refraction on the horizontal interface y = 0 is characterized by the relation

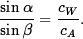
In words, this says that the sine of the angle of incidence is related to the sine of the angle of refraction just as the velocity of light in the primary media (water) is related to the velocity of light in the secondary media (air). This relation is known as Snell's Law.

The Brachistochrone
We will apply Snell's Law to the investigation of a famous problem suggested in 1690 by Johann Bernoulli. This problem gave birth to the Calculus of Variations - a powerful branch of mathematics. Bernoulli's problem is as follows: Suppose we have a heavy particle such as a steel ball which starts off at rest at point A. It then slides downward, under the force of gravity alone, along a frictionless track in a vertical plane along some curve through A and another fixed point B. The question is this: What shape should we make the curve if we want to minimize the time of the object's descent from A to B? The curve possessing this property is called a brachistochrone ().

Johann Bernoulli gave an exclusively beautiful solution of this problem. He knew from physics that a heavy particle will have a speed of

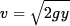(2)

at the vertical distance y measured downward from the particle's original location (Fig. 2). In other words, regardless of the shape of the particle's trajectory AB, its speed v depends only on the vertical distance y. We'll try to intuitively realize the significance of this fundamental fact.

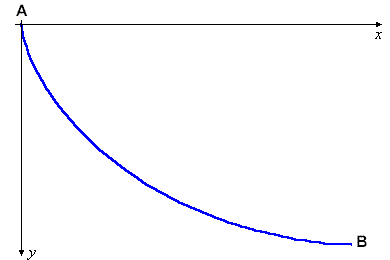
Figure 2: A brachistochrone

Let's split the vertical plane through the curve AB into a series of thin horizontal layers. The speed v can then be assumed to be constant within every layer, but this constant will vary as we move from one layer to another. Where did we encounter a similar situation? We saw something similar in the phenomenon of the refraction of sunlight that passes though a medium which varies from layer to layer. With this in mind, we can look at the curve AB differently. By Fermat's Principle, we can treat this curve as the trajectory of light which passes through an optically nonhomogeneous medium. In short, the light trajectory is a brachistochrone.

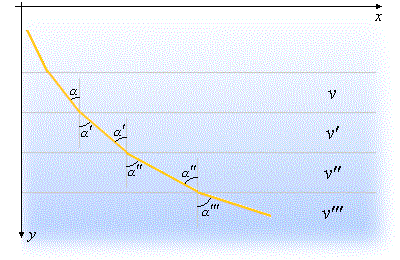
Figure 3: The trajectory of light through a nonhomogeneous medium

If we introduce a large number of layers, each with its own constant value of v, then we arrive at a number of uniform media differing only in the values of the velocity v of light. Within each layer, light will propagate along a straight line, but these lines will change direction at every interface.

If we now apply Snell's Law at each of these interfaces (see Fig. 3), we obtain

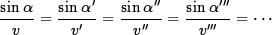
In other words, the ratio

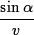
is exactly the same for all layers. If we consider infinitely many layers, this statement still remains valid and, in the limit, we obtain

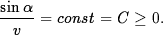(3)

We conclude that the unknown light path (i.e. the particle's trajectory) is governed by Eq. 3. This property allows for a nice analytical interpretation.

Problem Two
Assume that y = y(x) is an equation of a brachistochrone. Express sin as a function of y' = dy/dx, and use this expression along with Eq. 2 to represent the left hand side of Eq. 3 as a function of y and y'. You will obtain the relationship

F(y, y') = const.

(4)

After you construct Eq. 4, verify that it is satisfied by the curve y = y(x) given by the parametric equations

x = a ( - sin ) y = a (1 - cos )

This curve is called a cycloid. It represents the path a reflector makes if it is attached to a point on the rim of a bicycle wheel (Fig. 4). So, the brachistochrone appears to be a cycloid.

Figure 4: A cycloid

Back to the top