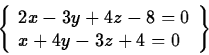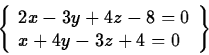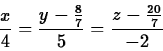Subsections

• Background
• Getting Started
• Exercises

Lines and Planes

Background

In three dimensions an equation with variables raised to the first power is a plane. Therefore to deal with lines, other equation forms must be used. By definition a line in three dimensions is the intersection of two planes. For example a line can be given as

$$\left\{\begin{array}{ll}2x-3y+4z-8=0\\ x+4y-3z+4=0\end{array}\right\}$$

Other methods of writing the same line can be used. By solving, the same line written symmetrically is

$$\frac{x}{4}=\frac{y-\frac{8}{7}}{5}=\frac{z-\frac{20}{7}}{-2}$$

or parametrically

$$\left[4t,\frac{8}{7}+5t,\frac{20}{7}-2t\right]$$

Looking again at the equations the plane equation is:

$$Ax+By+Cz+D=0$$

Note that the vector $<A,B,C>$ is the normal (perpendicular) vector to the plane. The symmetric line is:

$$\frac{x-x_1}{a}=\frac{y-y_1}{b}=\frac{z-z_1}{c}$$

Note that 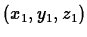$(x_1,y_1,z_1)$ is a point on the line and the vector 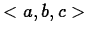$<a,b,c>$ is parallel to the line. Finally the parametric line is:

$$[x_1+at,y_1+bt,z_1+ct]$$

Knowing these facts and knowing which form to work with will help in solving three-dimensional problems.

Getting Started

To assist you, there is a worksheet associated with this lab that contains examples similar to some of the exercises. You can copy that worksheet to your home directory with the following command, which must be run in a terminal window, not in Maple.

cp /math/calclab/MA1024/lines_and_planes.mws My_Documents

Once you have read through the exercises, start up Maple, load the worksheet, and go through it carefully. Then you can start working on the exercises.

Exercises

1. Find the distance from the point 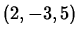$(2,-3,5)$ to the plane $3x+2y+6z=2$.
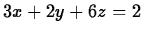   Remember that distance is always considered the perpendicular path. As a hint first find the intersection of this perpendicular line to the plane and then use the distance formula.
   Plot the perpedicular line and the plane.
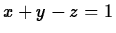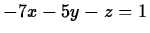2. Find the line parallel to the intersection of the two planes $x+y-z=1$ and $-7x-5y-z=1$ and passing through the point $(0,0,5)$.
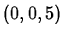   As a hint start with the normal vectors to the planes.
   Plot the two planes and the parallel line.