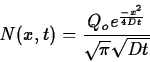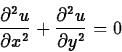Next: About this document ...
Up: lab_template
Previous: lab_template
Subsections
The purpose of this lab is to aquaint you with partial differential equations.
Second-order partial derivatives show up in many physical models such as heat, wave, or electrical potential equations. For example, the one-dimensional wave equation
can be solved by the displacement equation
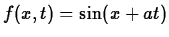 , or
, or
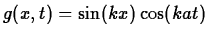 , or even
, or even
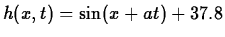 . To show this, enter the displacement equation and then show that both sides of the differential equation are equal.
. To show this, enter the displacement equation and then show that both sides of the differential equation are equal.
>f:=(x,t)->sin(x+a*t);
>g:=(x,t)->sin(k*x)*cos(k*a*t);
>h:=(x,t)->sin(x+a*t)+37.8;
>diff(f(x,t),t,t)-a^2*diff(f(x,t),x,x);
>diff(g(x,t),t,t)=a^2*diff(g(x,t),x,x);
>diff(h(x,t),t,t)=a^2*diff(h(x,t),x,x);
- Fick's second law of diffusion satisfies the partial differential equation
The function
denotes diffusion of a substance at a depth 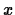 and time
and time 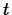 where
where 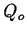 is the initial amount of the substance and
is the initial amount of the substance and 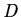 is the diffusion coefficient.
is the diffusion coefficient.
- A)
- Enter the function
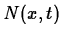 and show that the function satisfies the partial differential equation given above. (Note: you may need to use the simplify command on both sides of the equal sign.)
and show that the function satisfies the partial differential equation given above. (Note: you may need to use the simplify command on both sides of the equal sign.)
- B)
- If the initial amount of
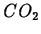 is
is
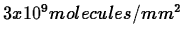 and the diffusion coefficients of
and the diffusion coefficients of 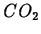 is
is 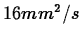 in the air and
in the air and 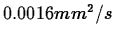 in the water, plot the surface concentration (N(0,t)) for ten seconds. There should be two plots; one titled diffusion through air and the other titled diffussion through water.
in the water, plot the surface concentration (N(0,t)) for ten seconds. There should be two plots; one titled diffusion through air and the other titled diffussion through water.
- C)
- Does the surface concentration increase or decrease for each as time increases? Explain why this is so.
Which concentration is higher over time? Explain why this is so.
- Determine which of the following functions satisfy Laplace's equation
- A)
-
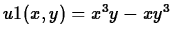
- B)
-
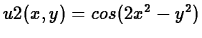
- C)
-
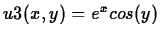
- D)
-
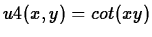
- Using a function from exercise 2 that you found satisfies the Laplace equation, answer the following without calculating the differential equation.
- A)
- Will the function plus
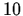 satisfy the Laplace equation? Why or why not?
satisfy the Laplace equation? Why or why not?
- B)
- Will the function plus
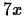 satisfy the Laplace equation? Why or why not?
satisfy the Laplace equation? Why or why not?
- C)
- Will the function plus
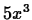 satisfy the Laplace equation? Why or why not?
satisfy the Laplace equation? Why or why not?



Next: About this document ...
Up: lab_template
Previous: lab_template
Jane E Bouchard
2006-11-01