Subsections

• Purpose
• Background
  • Volumes from double integrals
  
  
• Maple Commands
• Exercises

Double integrals with Maple

Purpose

The purpose of this lab is to acquaint you with using Maple to do double integrals.

Background

Volumes from double integrals

Suppose that $R$ is a rectangular region in the the $x-y$ plane, and that $f(x,y)$ is a continuous, non-negative function on $R$. Then the volume of the solid above $R$ and below $z=f(x,y)$ is given by the double integral

$$\int_R \! \int f(x,y) \, dA$$

You learned in class that such integrals can be evaluated by either of the iterated integrals

$$\int_a^b \left( \int_c^d f(x,y) \, dy \right) dx$$

or

$$\int_c^d \left( \int_a^b f(x,y) \, dx \right) dy$$

where the rectangle $R$ is defined by the inequalities $a \leq x \leq b$ and $c \leq y \leq d$.

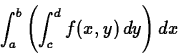
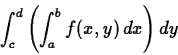
Following are examples of how to use Maple to compute double integrals. It also has an example of how to use Maple if the region of integration is of the more complicated form $R = \left\{(x,y): g_1(x) \leq y \leq g_2(x), a \leq x \leq b \right\}$. This is the case where the base of the solid is not rectangular, but is bounded by two curves $y=g_1(x)$ and $y=g_2(x)$. If $f(x,y)$ is as before, then the volume of the solid above $S$ and below $z=f(x,y)$ is given by

$$\int_a^b \left( \int_{g_1(x)}^{g_2(x)} f(x,y) \, dy \right) dx$$

The other case, where the region $R$ is $x$-simple can also be handled using Maple.

Maple Commands

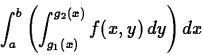
The main command for computing multiple integrals with Maple is the int command you are already familiar with. You simply use nested int commands and compute the integrals as iterated integrals. To integrate a function over a rectangular region, just nest the two int commands. The following command computes the integral $\int_0^1 \int_{-2}^1 x^2+y^2 \,dx\, dy$

>int(int(x^2+y^2,x=-2..1),y=0..1);

This command computes the same integral, but in the opposite order. that is, it computes $\int_{-2}^1 \int_0^1 x^2+y^2 \, dy \, dx$

>int(int(x^2+y^2,y=0..1),x=-2..1);

Maple can also compute double intgrals where the limits are not constants. For example, suppose you wanted to compute the integral of 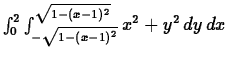$f(x,y)=x^2+y^2$ over the disk in the x-y plane whose boundary is the circle $(x-1)^2+y^2=1$. This can be treated as a region that is y-simple by solving the equation of the circle for $y$. This gives two functions $y=\sqrt{1-(x-1)^2}$ and $y = -\sqrt{1-(x-1)^2}$, which are just the upper and lower halves of the circle. The integral would be $\int_0^2\int_{-\sqrt{1-(x-1)^2}}^{\sqrt{1-(x-1)^2}}x^2+y^2\,dy\,dx$ and the Maple command to do this integral is

>int(int(x^2+y^2,y=-sqrt(1-(x-1)^2)..sqrt(1-(x-1)^2)),x=0..2);

You can also use Maple to compute double integrals over regions that are x-simple. Suppose we repeat the previous calculation, but solve the equation for 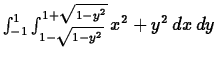$x$ instead of $y$. This gives the two functions $x=1+\sqrt{1-y^2}$ and $x=1-\sqrt{1-y^2}$ for the right and left halves of the circle. The integral would be $\int_{-1}^1\int_{1-\sqrt{1-y^2}}^{1+\sqrt{1-y^2}}x^2+y^2\,dx\,dy$ and the Maple command to do this is:

>int(int(x^2+y^2,x=1-sqrt(1-y^2)..1+sqrt(1-y^2)),y=-1..1);

Exercises

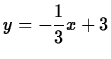1. Let $R$ be the region in the $xy$ plane bounded by the two curves $y=\sqrt{9-x^2}$ and $$y= -\frac{1}{3}x+3$$. Use a double integral to compute the area of the region. Include a plot of the region $R$ in your worksheet.

2. Use a double integral to find the volume of the region bounded by the two paraboloids $z=x^2+3y^2$ and $z=16-2x^2-y^2$.