


Next: About this document ...
Up: lab_template
Previous: lab_template
Subsections
The purpose of this lab is to acquaint you with some common three-dimensional shapes.
Three-dimensional curves can be entered as a function (or functions) of two variables or as an expression.
>with(plots):
>f:=(x,y)->25-x^2+1/300*y^4-y^2;
>blob:=z=x^2+3.7*y^2;
>plot3d(f(x,y),x=-10..10,y=-15..15,axes=boxed);
>implicitplot3d({f(x,y)=z,blob},x=-10..10,y=-15..15,z=-200..200,axes=boxed,
numpoints=2000,style=wireframe,color=aquamarine);
Remember the definition of a function when entering your shape. For example, the sphere can be entered as two functions or as one implicit expression.
>f:=(x,y)->sqrt(-x^2-y^2+1);g:=(x,y)->-sqrt(-x^2-y^2+1);
>plot3d({f(x,y),g(x,y)},x=-1..1,y=-1..1,numpoints=15000,scaling=constrained,
style=patchnogrid,axes=boxed);
>sphere:=x^2+y^2+z^2=1;
>implicitplot3d(sphere,x=-1..1,y=-1..1,z=-1..1,axes=boxed);
To look at the cross-section of the sphere you cut the sphere along a plane - i.e. you hold a variable constant. So the intersection of the sphere and the 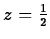 plane is:
plane is:
>sph_at_half:=x^2+y^2+1/2^2=1;
>implicitplot(sph_at_half,x=-1..1,y=-1..1);
Notice that the plot is a two-dimensional circle. To intersect vertical planes hold the 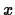 or
or 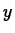 constant. Notice this can be done using the function or expression.
constant. Notice this can be done using the function or expression.
>plot({f(1/3,y),g(1/3,y),f(-2/3,y),g(-2/3,y)},y=-1..1,labels=[y,z]);
>sph_y1:=x^2+0.6^2+z^2=1;sph_y2:=x^2+0.8^2+z^2=1;
>implicitplot({sph_y1,sph_y2},x=-1..1,z=-1..1);
Other three-dimensional shapes can be made from known conic sections. A few of these will be analyzed in the exercises.
(Note: In all plots include the option scaling=constrained).
- Given
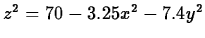
- A)
- Plot the three-dimensional shape over the intervals
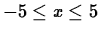 ,
,
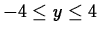 , and
, and
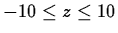 .
.
- B)
- Is the given equation a function?
- C)
- Plot the intersections of this shape and two planes parallel to the z-axis. What two-dimensional shapes are graphed?
- D)
- Plot the intersections of this shape and two planes parallel to the y-axis. What two-dimensional shapes are graphed?
- E)
- Plot the intersections of this shape and two planes parallel to the x-axis. What two-dimensional shapes are graphed?
- F)
- What three-dimensional shape is the equation (a sphere, a paraboloid, an ellipsoid, an hyperboloid, a parabolic saddle, or an hyperbolic saddle)?
- Given
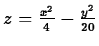
- A)
- Plot the three-dimensional shape over the intervals
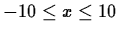 ,
,
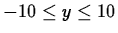 , and
, and
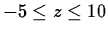 .
.
- B)
- Is the given equation a function?
- C)
- Plot the intersections of this shape and two planes parallel to the z-axis. What two-dimensional shapes are graphed?
- D)
- Plot the intersections of this shape and two planes parallel to the y-axis. What two-dimensional shapes are graphed?
- E)
- Plot the intersections of this shape and two planes parallel to the x-axis. What two-dimensional shapes are graphed?
- F)
- What three-dimensional shape is the equation (a sphere, a paraboloid, an ellipsoid, an hyperboloid, a parabolic saddle, or an hyperbolic saddle)?
- Given
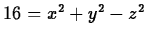
- A)
- Plot the three-dimensional shape over the interval
![$[-10,10]$](img13.png) for all three variables..
for all three variables..
- B)
- Is the given equation a function?
- C)
- Plot the intersections of this shape and two planes parallel to the z-axis. What two-dimensional shapes are graphed?
- D)
- Plot the intersections of this shape and two planes parallel to the y-axis. What two-dimensional shapes are graphed?
- E)
- Plot the intersections of this shape and two planes parallel to the x-axis. What two-dimensional shapes are graphed?
- F)
- What three-dimensional shape is the equation (a sphere, a paraboloid, an ellipsoid, an hyperboloid, a parabolic saddle, or an hyperbolic saddle)?



Next: About this document ...
Up: lab_template
Previous: lab_template
Jane E Bouchard
2006-01-13
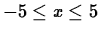 ,
,
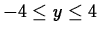 , and
, and
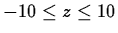 .
.
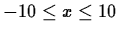 ,
,
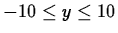 , and
, and
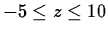 .
.
![$[-10,10]$](img13.png) for all three variables..
for all three variables..