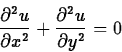Next: About this document ...
Up: lab_template
Previous: lab_template
Subsections
The purpose of this lab is to aquaint you with partial differential equations.
Second-order partial derivatives show up in many physical models such as heat, wave, or electrical potential equations. For example, the one-dimensional wave equation
can be solved by the displacement equation
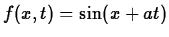 , or
, or
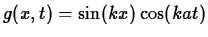 , or even
, or even
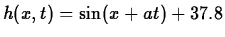 . To show this, enter the displacement equation and then show that both sides of the differential equation are equal.
. To show this, enter the displacement equation and then show that both sides of the differential equation are equal.
>f:=(x,t)->sin(x+a*t);
>g:=(x,t)->sin(k*x)*cos(k*a*t);
>h:=(x,t)->sin(x+a*t)+37.8;
>diff(f(x,t),t,t)-a^2*diff(f(x,t),x,x);
>diff(g(x,t),t,t)=a^2*diff(g(x,t),x,x);
>diff(h(x,t),t,t)=a^2*diff(h(x,t),x,x);
- The function
denotes temperature at a depth 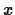 and time
and time 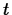 where the seasonal variation of the surface
where the seasonal variation of the surface 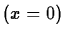 temperature is
temperature is
Where 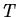 is the annual average surface temperature and
is the annual average surface temperature and 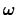 is chosen such that the period is one year.
is chosen such that the period is one year.
- A)
- Enter the function
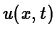
- B)
- Show that the function satisfies the surface condition (i.e.
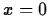 ).
).
- C)
- Show that the function
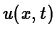 satisfies that one-dimensional heat equation
satisfies that one-dimensional heat equation
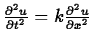 .
.
- D)
- Enter the following data into memory (Do this after completeing parts A, B, and C, or you will need to re-initialize the constants).

- The thermal conductivity of brick is
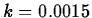 .
.

- The average temperature of the surface temperature is
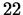 degrees celsius, please enter as
degrees celsius, please enter as 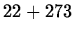 as the conductivity uses units of Kelvin.
as the conductivity uses units of Kelvin.

- The surface area of a brick is
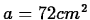

-
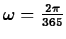
- E)
- Plot the surface temperature
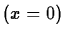 of a brick for one year (
of a brick for one year (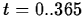 ). To make the temperature axis celsius, plot the function minus 273.
). To make the temperature axis celsius, plot the function minus 273.
- F)
- From your graph, what is the approximate temperature variation of the surface of the brick?
- G)
- Plot the temperature of the inside of the brick with dimensions six by six by twelve (i.e. depth =
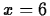 ). Remember to plot using celsius.
). Remember to plot using celsius.
- H)
- From your graph, what is the temperature variation of the inside of the brick?
- Determine which of the following functions satisfy Laplace's equation
- A)
-
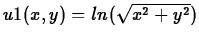
- B)
-
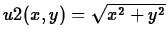
- C)
-
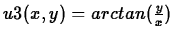
- D)
-
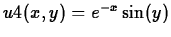
- Using a function from exercise 2 that you found satisfies the Laplace equation, answer the following without calculating the differential equation.
- A)
- Will the function plus
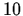 satisfy the Laplace equation? Why or why not?
satisfy the Laplace equation? Why or why not?
- B)
- Will the function plus
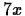 satisfy the Laplace equation? Why or why not?
satisfy the Laplace equation? Why or why not?
- C)
- Will the function plus
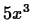 satisfy the Laplace equation? Why or why not?
satisfy the Laplace equation? Why or why not?



Next: About this document ...
Up: lab_template
Previous: lab_template
Jane E Bouchard
2006-01-20