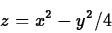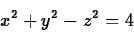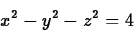Subsections

• Introduction
• Background
• Exercises

Surfaces

Introduction

The purpose of this lab is to acquaint you with some common three-dimensional shapes.

Background

Three-dimensional curves can be entered as a function (or functions) of two variables or as an expression.

>with(plots):
>f:=(x,y)->25-x^2+1/300*y^4-y^2;
>blob:=z=x^2+3.7*y^2-100;
>plot3d(f(x,y),x=-10..10,y=-15..15,axes=boxed);
>implicitplot3d([f(x,y)=z,blob],x=-10..10,y=-15..15,z=-200..200,axes=boxed,
numpoints=4000,style=[patchnogrid,wireframe],color=[pink,blue]);

Remember the definition of a function when entering your shape. For example, the sphere can be entered as two functions or as one implicit expression.

>f:=(x,y)->sqrt(-x^2-y^2+1);g:=(x,y)->-sqrt(-x^2-y^2+1);
>plot3d({f(x,y),g(x,y)},x=-1..1,y=-1..1,numpoints=15000,scaling=constrained,
style=patchnogrid,axes=boxed);
>h:=x^2+y^2+z^2=1;
>implicitplot3d(h,x=-1..1,y=-1..1,z=-1..1,axes=boxed);

To look at the cross-section of the sphere you cut the sphere along a plane - i.e. you hold a variable constant. So the intersection of the sphere and the 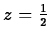$z=\frac{1}{2}$ plane is:

> implicitplot(subs(z=1/2,h),x=-1..1,y=-1..1);

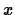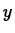Notice that the plot is a two-dimensional circle. To intersect vertical planes hold the $x$ or $y$ constant.

> implicitplot({subs(x=0,h),subs(x=1/3,h)},y=-1..1,z=-1..1,labels=[y,z]);

Other three-dimensional shapes can be made from known conic sections. A few of these will be analyzed in the exercises.

Exercises

(Note: In all plots include the option scaling=constrained).

1. For the given equations below, plot 2 two-dimensional level curves parallel to the 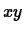$xy$ plane and then plot 2 two-dimensional cross sections in the 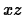$xz$ plane and then the 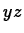$yz$ plane. State the shapes for each 2-d graph.Then identify the type or shape of the quadric surface, ie. a sphere, cylinder, cone, elliptic cone, paraboloid, elliptic parabaloid, ellipsoid, hyperboloid of one sheet, hyperboloid of two sheets, or a hyperbolic parabaloid (saddle). Once you have determined the shape of the surface, supply a three dimensional plot to support your conclusion.

   a)

   
   

   $$z=x^2-y^2/4$$

   
   

   b)

   
   

   $$x^2+y^2-z^2=4$$

   
   

   c)

   
   

   $$x^2-y^2-z^2=4$$