 i +
i +
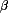 j +
j +
 k
.
k
.
- Please plot r(t) in the xy-plane.
- Please show that the graph of r(t) is the circle
of radius 3 centered at the point (2, -4). That is, show that the
component functions x(t) and y(t) of
r(t) satisfy the equation
(x - 2)2 + (y + 4)2 = 9 for all values of t. - Show that the speed is constant and explain why this is so. Then find a value of the constant b that gives a speed of 18.
- Using Maple, please show that r
 (t) is perpendicular to
r
(t) is perpendicular to
r
 (t).
(t).
- If a = 3, please find the smallest value of t > 0 for which the two particles collide.
- Is it possible to find a positive real number a for which the two particles do not collide for any value of t > 0? Explain your answer.
In 1974 Evel Knievel attempted a skycycle ride across the Snake River, and at the time there was a great deal of hype about "will he make it?" If the angle of the launching ramp was 45° and if the horizontal distance the skycycle needed to travel was 4,700 ft, at what speed did Evel have to leave the ramp in order to make it across the Snake River Canyon?Hint: Assume that the opposite edges of the canyon are at the same height.