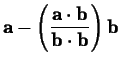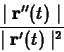Maple has several useful functions for working with vectors. This lab provides a brief introduction to the most basic commands. All of the commands used in this lab come from the Maple linalg and the CalcP packages, which must be loaded before any of the commands can be used.
Here is a list of the Maple functions we will be using from the linalg package. Note that these functions form only a small subset of the package, which is designed primarily for linear algebra. Examples for some of the commands are given below, more examples can be found in the help screens for each command. Several of these commands appeared in the previous lab, so you might want to refer back to it.
This is a list of the commands from the CalcP package that are appropriate for this lab. Several should be familiar from the previous lab.
The first set of examples below demonstrates how to compute linear combinations of vectors, dot and cross products, magnitudes, and vector components for fixed vectors.
> with(linalg):
Warning: new definition for norm Warning: new definition for trace
> a := vector([2,13,-6]);
> b := vector([5,-4,17]);
> evalm(a+b);
> evalm(5*a-2*b);
> innerprod(a,b);
> crossprod(a,b);
> crossprod(b,a);
> innerprod(a,crossprod(a,b));
The next two commands show two different ways to compute the magnitude
of a vector. The first way uses the norm
command. Note the 2 as the second argument of the command. This
2 has to be there, or else Maple uses a different norm
than the one we want. The second way, using the fact that
![]() , is probably the
preferred one.
, is probably the
preferred one.
> norm(a,2);
> sqrt(innerprod(a,a));
As we've seen in class, computing the curvature, ![]() , and the
unit normal and tangent vectors is a tedious process, even for the
simplest of curves. Fortunately, Maple procedures can be written to do
these calculations and this lab will introduce you to the ones that we
have written here at WPI as part of the CalcP package. As usual,
before you can use any of these commands, you must load the package with the
following command. Since some of the commands use the linalg
package, it is probably a good idea to load it as well.
, and the
unit normal and tangent vectors is a tedious process, even for the
simplest of curves. Fortunately, Maple procedures can be written to do
these calculations and this lab will introduce you to the ones that we
have written here at WPI as part of the CalcP package. As usual,
before you can use any of these commands, you must load the package with the
following command. Since some of the commands use the linalg
package, it is probably a good idea to load it as well.
> with(linalg):
Warning: new definition for norm Warning: new definition for trace
> with(CalcP):
The next few commands deal with a simple example of a curve known as a helix. In one of the exercises, you will be investigating a more general version of a helix, so you are encouraged to pay close attention to the following examples. Note the use of the axes option in the VPlot command. Including axes in a plot is often helpful in visualizing a curve in three dimensions. Also, recall that if you click on a plot, controls appear in the context bar that allow you to modify the plot, including changing the axes style and rotating the plot. If you have trouble doing this, ask for help.
Note also
that we've used the linalg command vector to define
the function ![]() instead of the simpler list notation we
used in the previous lab. The commands in the CalcP package
can handle either notation, but the commands in the linalg
package require you to use the vector command to define fixed
vectors or vector-valued functions.
instead of the simpler list notation we
used in the previous lab. The commands in the CalcP package
can handle either notation, but the commands in the linalg
package require you to use the vector command to define fixed
vectors or vector-valued functions.
> h := t -> vector([cos(t),sin(t),t]);
> VPlot(h(t),t=0..4*Pi,axes=NORMAL);
> ParamPlot3D(h(t),t=0..4*Pi);
> Curvature(h(t),t);