One of the most valuable services provided by computer software such as Maple is that it allows us to produce intricate graphs with a minimum of effort on our part. This becomes especially apparent when it comes to functions of two variables, because there are many more computations required to produce one graph, yet Maple performs all these computations with only a little guidance from the user.
Two common ways of representing the graph of a function of two variables
are the surface plot and the contour plot. The first is simply a
representation of the graph in three-dimensional space. The second,
draws the level curves ![]() for several values of
for several values of ![]() in the
in the
![]() -plane. We will explore how to produce these kinds of graphs in
Maple, and how to use the graphs to study the functions.
-plane. We will explore how to produce these kinds of graphs in
Maple, and how to use the graphs to study the functions.
You can define functions of more than one variable in much the same way as you defined functions of a single variable:
> f := (x,y) -> x^2 + y^2; > f(3,-1); > g := (a,b,c,d,e) -> a*b^2 - sin(c+d)/e;
The following commands are useful for working with functions of two variables in Maple.
> plot3d(x^2-y^2, x=-1..1, y=-1..1); > f := (x,y) -> x/2 - y + 3; > plot3d(f, 0..2, -1..1);The default viewing angle is from a direction 45 degrees between the positive
orientation=[a,b]. The
first number is the polar angle, measured counterclockwise from
the positive
You can also select a viewpoint using the mouse.
Click the mouse on a three-dimensional graph,
and notice the context bar that appears between the tool bar
and the Maple input/output window.
Hold down the button as you move the mouse, and you'll see
the surface from different angles. You'll also
see the numbers in the upper left-hand side of the context
bar, labeled ![]() and
and ![]() ,
change accordingly. They correspond to the two numbers in
the
,
change accordingly. They correspond to the two numbers in
the orientation option. Note that the other buttons
in the context bar can be used to change various aspects of
the plot, including choosing the plot style and among several
different choices for axes.
The number of grid points in the plot can be changed with the grid=[x,y] option. You may want to increase the number of grid points if your plot appears rough, or has a lot of oscillation; you may want to use a smaller number if the function is reasonably smooth and you want to shorten calculation times.
> plot3d(x^2-y^2,x=-1..1,y=-1..1,orientation=[45,45]); > plot3d(x^2-y^2,x=-1..1,y=-1..1,orientation=[45,20]); > plot3d(x^2-y^2,x=-1..1,y=-1..1,orientation=[45,-45]); > plot3d(x^2-y^2,x=-1..1,y=-1..1,orientation=[110,45]); > plot3d(x^2-y^2,x=-1..1,y=-1..1,grid=[10,10]); > plot3d(x^2-y^2,x=-1..1,y=-1..1,grid=[25,40]); > plot3d(x^2-y^2,x=-1..1,y=-1..1,axes=NORMAL]For more information on options, you can type ?plot3d,option.
Note that you can use the context bar instead of optional arguments to the plot3d command to customize your plot. Saving your worksheet after you have made changes will save the plot as it last appeared. However, if you need to run the plot3d command again, any customizations you made with the context bar will be lost. The safest approach is to use the context bar to experiment with your plot until you are satisfied with it. Then add options to your plot3d command that will give you the same plot, for example by specifying the orientation or axes arguments in your command.
with(plots) before using the command. The basic
syntax is the same as for plot3d.
> with(plots): > contourplot(x^2-y^2,x=-1..1,y=-1..1); > f := (x,y) -> x/2 - y + 3; > contourplot(f,0..2,-1..1);Maple's default is to produce ten contours. This can be changed using the option
contours=n. Maple chooses the > contourplot(x^2-y^2,x=-2..2,y=-2..2); > contourplot(x^2-y^2,x=-2..2,y=-2..2,contours=6); > contourplot(x^2-y^2,x=-2..2,y=-2..2,contours=[6]); > contourplot(x^2-y^2,x=-2..2,y=-2..2,contours=[-1,0,1,2]);
> implicitplot3d(y^2+z^2=2,x=0..2,y=-2..2,z=-2..2);Getting a good plot using this command can be a little tricky because you have to come up with good guesses for the ranges for
> plot3d(1,theta=0..2*Pi,z=-1..1,coords=cylindrical);The next command plots the cone
> plot3d(1-z,theta=0..2*Pi,z=-1..1,coords=cylindrical);The plot3d command expects your equation for the surface to be of the form
Plotting a surface in spherical coordinates is very similar. Maple
expects the equation of the surface to be in the form
![]() . Again, the order of
. Again, the order of ![]() and
and ![]() is important
when specifying ranges. The following command
plots the unit sphere.
is important
when specifying ranges. The following command
plots the unit sphere.
> plot3d(1,theta=0..2*Pi,phi=0..Pi,coords=spherical);Many surfaces can be represented in more than one coordinate system. For example, the following command plots the same cylinder of radius 1 that we plotted before, but in spherical coordinates.
> plot3d(1/sin(phi),theta=0..2*Pi,phi=Pi/4..3*Pi/4,coords=spherical);
The implicitplot3d command can also be used to plot relations
in terms of cylindrical or spherical coordinates. You just use the
same coords optional argument that you used for the
plot3d command. The only tricky part
is that it expects you to give the ranges in a certain order. For
example, in cylindrical coordinates it expects the range for ![]() first, then the range for
first, then the range for ![]() , and finally the range for
, and finally the range for
![]() . Other orders can give incorrect results. For spherical
coordinates, the order must be
. Other orders can give incorrect results. For spherical
coordinates, the order must be
![]() .
.
> plot3d([s,2*cos(t),2*sin(t)],s=0..2,t=0..2*Pi);We used the implicitplot3d command above to plot this same cylinder. An advantage of using a parametric plot is that you usually know what ranges to use for your parameters to get the plot you want.
As a final example of a parametric surface, we present the torus, or doughnut if you are feeling hungry.
> plot3d([4*cos(s)+cos(t)*cos(s),4*sin(s)+cos(t)*sin(s),sin(t)], s=0..2*Pi,t=0..2*Pi,style=patch);
The unfortunate thing about this problem is that modifications you might have made to your plots using the mouse or the context bar are lost. This is why it is a good idea to first experiment with your plot using the mouse and the context bar but, once you have the plot looking the way you want it, to include your modifications in the plot command.
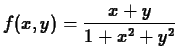 ,
for
,
for