


Next: About this document ...
Up: lab_template
Previous: lab_template
Subsections
The purpose of this lab is to introduce you to some of the Maple
commands that can be used to plot surfaces in three dimensions.
To assist you, there is a worksheet associated with this lab that
contains examples and even solutions to some of the exercises. You can
copy that worksheet to your home directory with the following command,
which must be run in a terminal window, not in Maple.
cp /math/calclab/MA1024/Surf_start.mws ~
You can copy the worksheet now, but you should read through the lab
before you load it into Maple. Once you have read to the exercises,
start up Maple, load
the worksheet Surf_start.mws, and go through it
carefully. Then you can start working on the exercises.
The graph of a function of a single real variable is a set of
points 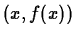 in the plane. Typically, the graph of such a function
is a curve. For functions of two variables in Cartesian
coordinates, the graph is a set of points
in the plane. Typically, the graph of such a function
is a curve. For functions of two variables in Cartesian
coordinates, the graph is a set of points 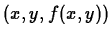 in
three-dimensional space. For this reason, visualizing
functions of two variables is usually more difficult. For students,
it is usually even more difficult if the surface is described in
terms of polar or spherical coordinates.
in
three-dimensional space. For this reason, visualizing
functions of two variables is usually more difficult. For students,
it is usually even more difficult if the surface is described in
terms of polar or spherical coordinates.
One of the most valuable services provided by computer software such
as Maple is that it allows us to produce intricate graphs with a minimum
of effort on our part. This becomes especially apparent when it comes
to functions of two variables, because there are many more computations
required to produce one graph, yet Maple performs all these computations
with only a little guidance from the user.
The simplest way of describing a surface in Cartesian coordinates is
as the graph of a function 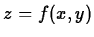 over a domain, e.g. a set of
points in the
over a domain, e.g. a set of
points in the 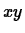 plane. The domain can have any shape, but a
rectangular one is the easiest to deal with.
Another common, but more difficult way of describing a surface is as
the graph of an equation
plane. The domain can have any shape, but a
rectangular one is the easiest to deal with.
Another common, but more difficult way of describing a surface is as
the graph of an equation 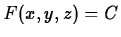 , where
, where 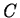 is a constant. In
this case, we say the surface is defined implicitly. A third way of
representing a surface
is a constant. In
this case, we say the surface is defined implicitly. A third way of
representing a surface 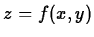 is through the use of level
curves. The idea is that a plane
is through the use of level
curves. The idea is that a plane 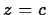 intersects the
surface in a curve. The projection of this curve on the
intersects the
surface in a curve. The projection of this curve on the 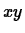 plane is
called a level curve. A collection of such curves for different values
of
plane is
called a level curve. A collection of such curves for different values
of 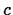 is a representation of the surface called a contour plot.
is a representation of the surface called a contour plot.
Some surfaces are difficult to describe in Cartesian coordinates, but
easy to describe using either cylindrical or spherical
coordinates. The obvious examples are cylinders and spheres, but there
are many other situations where these coordinate systems are useful.
- Generate a surface plot and contour plot for the
following function on the given domain:
for
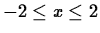 and
and
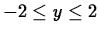 .
.
- A
- What does the contour plot look like in the regions where
the surface plot has a steep incline? What does it look like
where the surface plot is almost flat?
- B
- What can you say about the surface plot in a region where the
contour plot looks like a series of nested circles?
- Generate a surface plot for the following functions on the domains given.
- A
-
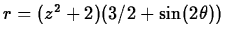 for
for
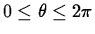 and
and
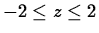 . Use cylindrical coordinates.
. Use cylindrical coordinates.
- B
-
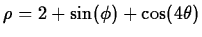 for
for
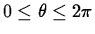 and
and
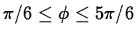 . Use spherical coordinates.
. Use spherical coordinates.
- Consider the following function
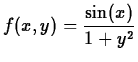 for
for
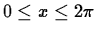 and
and
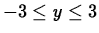 which looks like a deep valley with a mountain opposite it. Is is possible to find a path from the point
which looks like a deep valley with a mountain opposite it. Is is possible to find a path from the point 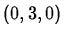 to
to 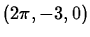 such that the value of
such that the value of 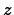 is always between
is always between 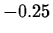 and
and 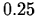 ? You do not have to find a formula for your path, but you must present convincing evidence that it exists. For example, you might want to sketch your path in by hand on an appropriate countour plot.
? You do not have to find a formula for your path, but you must present convincing evidence that it exists. For example, you might want to sketch your path in by hand on an appropriate countour plot.



Next: About this document ...
Up: lab_template
Previous: lab_template
Jane E Bouchard
2005-03-07
![]() over a domain, e.g. a set of
points in the
over a domain, e.g. a set of
points in the ![]() plane. The domain can have any shape, but a
rectangular one is the easiest to deal with.
Another common, but more difficult way of describing a surface is as
the graph of an equation
plane. The domain can have any shape, but a
rectangular one is the easiest to deal with.
Another common, but more difficult way of describing a surface is as
the graph of an equation ![]() , where
, where ![]() is a constant. In
this case, we say the surface is defined implicitly. A third way of
representing a surface
is a constant. In
this case, we say the surface is defined implicitly. A third way of
representing a surface ![]() is through the use of level
curves. The idea is that a plane
is through the use of level
curves. The idea is that a plane ![]() intersects the
surface in a curve. The projection of this curve on the
intersects the
surface in a curve. The projection of this curve on the ![]() plane is
called a level curve. A collection of such curves for different values
of
plane is
called a level curve. A collection of such curves for different values
of ![]() is a representation of the surface called a contour plot.
is a representation of the surface called a contour plot.
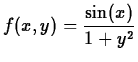 for
for