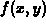 is a continuous, non-negative function on D. Then the
volume of the solid above D and below
is a continuous, non-negative function on D. Then the
volume of the solid above D and below 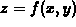 is given by the
double integral
is given by the
double integral
Suppose that D is a rectangular region in the the x-y plane, and
that 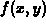 is a continuous, non-negative function on D. Then the
volume of the solid above D and below
is a continuous, non-negative function on D. Then the
volume of the solid above D and below 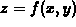 is given by the
double integral
is given by the
double integral

We learned in class that such integrals can be evaluated by either of the iterated integrals
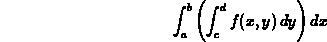
or
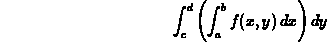
where the rectangle D is defined by the inequalities 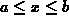 and
and 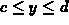 .
.
Using Maple to evaluate double integrals proceeds in exactly the same fashion. For example, the following Maple commands show the computation of

for both orders of integration.
> int(int(x^2+y^2,x=-2..1),y=0..1);

> int(int(x^2+y^2,y=0..1),x=-2..1);

More complicated integrals are handled similarly. Suppose that we have
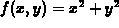 and we want to know the volume of the solid
between the region in the xy plane bounded by the circle
and we want to know the volume of the solid
between the region in the xy plane bounded by the circle
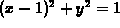 and the graph of
and the graph of 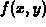 . Then an appropriate
integral is
. Then an appropriate
integral is
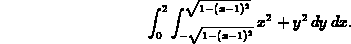
Using Maple, we calculate this as
> int(int(x^2+y^2,y=-sqrt(1-(x-1)^2)..sqrt(1-(x-1)^2)),x=0..2);
