Examples

All of the Maple commands necessary for this lab have already been seen before.

• Find where y=cos(x) and intersect.

    > solve(cos(x)=x^2+2*x-3,x);
  

    > fsolve(cos(x)=x^2+2*x-3,x);
  

  

    > plot({cos(x),x^2+2*x-3},x=-5..5);
  

    > fsolve(cos(x)=x^2+2*x-3,x=-5..0);
  

  

  These two functions intersect at approximately x=1.1085 and x=-2.7534. This can be viewed on the graph.

• Find the first order partial derivatives for the following function.

  

  Recall that there are multiple ways of doing this. These are two of the ways seen in the past.

  • The first way is using the diff command.

      > f:=(x,y)->x^2*y^2+y*sin(x);
    

    

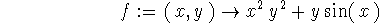
      > f_x:=diff(f(x,y),x);
    

    

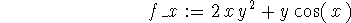
      > f_y:=diff(f(x,y),y);
    

    

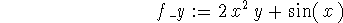
  • The second method is using the D command. Notice that the number in the square braces corresponds to the variable in that position when defining the function.

      > f_x:=D[1](f);
    

    

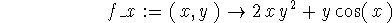
      > f_y:=D[2](f);
    

    

• Compute this integral

  

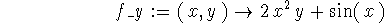
  over the region R where and

    > inner:=int(2*x*y/(x^2+1),x=0..1);
  

  

    > outer:=int(inner,y=1..3);
  

  

    > evalf(outer);
  

  

  The exact value of this integral is . The decimal approximation to this integral is 2.7726. Note that this integral could be computed in one step.

    > int(int(2*x*y/(x^2+1),x=0..1),y=1..3);
  

  

• Compute the following double integral.

  

    > inner:=int(exp(y-x),y=x..2*x);
  

  

    > outer:=int(inner,x=0..1);
  

  

    > evalf(outer);
  

  

  The exact value of this integral is e-2. The decimal approximation to this integral is .7183. Or to save some steps, the following Maple command can be executed.

    > int(int(exp(y-x),y=x..2*x),x=0..1);