


Next: About this document ...
Up: Labs and Projects for
Previous: Background
- 1.
- For each of the following functions,
- i
- Print out a plot of the level curves.
- ii
- Calculate the partial derivatives fx and fy at the given points and for each point, build the gradient vector:
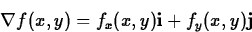
(You may use the grad command in Maple, but you will have to look up its syntax in Maple Help.)
- iii
- Sketch arrows (vectors) by hand at each of the chosen points in part b showing the direction of the gradient and explain why the gradient vectors are perpendicular to the level curves (you may have to scale the gradient vector).
- (a)
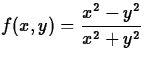 , at (10,2), (-10,2), (-10,-2), and (10,-2)
, at (10,2), (-10,2), (-10,-2), and (10,-2)
- (b)
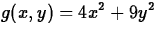 , at (2,4), (-2,4), (-2,-4), and (2,-4)
, at (2,4), (-2,4), (-2,-4), and (2,-4)
- (c)
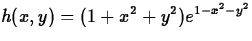 at (1,1), (-1,1), (-1,-1), and (1,-1)
at (1,1), (-1,1), (-1,-1), and (1,-1)
- 2.
- Find the absolute extrema of each of the following functions on the closed bounded set S in the xy-plane.
- (a)
- f(x,y) = x2 - 4xy +y3 + 4y where S is the square region
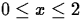 ,
, 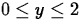 .
. - (b)
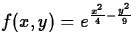 where S is the region
where S is the region 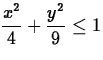 .
.
- 3.
- Find and classify the critical points of the following functions as a relative maximum, relative minimum, or saddle point.
- (a)
- f(x,y) = x3 + y3 - 3x2 - 18y2 + 81y + 7
- (b)
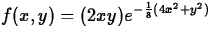



Next: About this document ...
Up: Labs and Projects for
Previous: Background
Christine M Palmer
3/31/1998
![]()
![]()
![]()
![]()
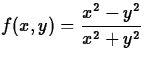 , at (10,2), (-10,2), (-10,-2), and (10,-2)
, at (10,2), (-10,2), (-10,-2), and (10,-2)
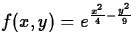 where S is the region
where S is the region 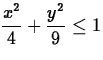 .
.