MA2051 - Ordinary Differential Equations
Sample Exam #1 - A96

Originally Given 1993 A Term 


 



TEST I

Covers 1.1-1.3, 2.1-2.3, 3.1-3.3.2, 3.5, 3.7-3.8, 4.1-4.2.1.


Instructions: Do your work on the paper provided.  Put your
name and section number on that paper.  Work neatly.  Show your work. 


JUSTIFY YOUR ANSWERS.








	1 (25 pts) 

    The kettle of a 
	popcorn machine in a movie theater is fed a continuous steam of 
	unpopped corn kernels.  Each minute a fixed fraction of the kernels 
	already in the kettle are ejected from the kettle as they pop.
	

	Let n(t) denote the number of unpopped kernels in the kettle at 
	time t.  Let A be the rate (kernels per minute) at which kernels 
	are added to the kettle.
	

    	Follow the steps below to derive a model for the number of unpopped 
	kernels in the kettle.
	

	A)
	

    	Write an expression for the rate at which kernels are added to the kettle.
    	

	B)
	
 Write an expression for the number of kernels which are 
    	added over a time interval of length  .
	

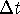	C)
	

	Write an expression for the rate at which kernels are 
	removed from the kettle because they have popped.
	

	D)
	

	Write an expression for the number of kernels which are removed over a time 
	interval of length  .
    	

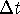	E)
	
 The law of conservation of popcorn states that the change in 
    	the number of kernels in the kettle over time 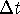 tex2html_wrap_inline47  equals the 
    	number of kernels added to the kettle minus the number of kernels 
    	removed.  Use this law and the results of the previous steps to 
    	derive a differential equation for n(t), the number of kernels in 
    	the kettle.  Complete the model by adding an appropriate initial 
    	condition.








	2 (20 pts) 


	Recent data suggests that a simple equation modeling the population of the world is 
	P' = 0.0165 P.  (Time is measured in years.)  Use one step of Euler's 
	method to estimate how much time will pass until the population of 
	the world has doubled.








	3 (35 pts) 

  
	Find the indicated solutions.


    

	A)
    

	Find a particular solution, a homogeneous solution, and a 
    	general solution of y' = ky - 2t.


    

	B)
    
 
	Find the solution of the initial value problem y' = ky - 2t,
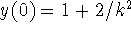	tex2html_wrap_inline61.


    

	C)
    
 
	Suppose you know that a solution of y' = ky + F(t) is the 
    	function Z(t) and that Z(0) = -4.  Find a general solution of
    	y' = ky + F(t) and find the solution of the initial value problem 
    	y' = ky + F(t), y(0) = 6; write these solutions in terms of 
    	Z(t).








	4 (20 pts) 

  Consider the equation y' = 2y - M; M is a constant.


    

	A)
    
 
	Find the steady state(s) of this equation.


    

	B)
    
 
	Determine the stability of the steady state(s).










  

    

© 1996 by Will Brother.
All rights Reserved. File last modified on September 16, 1996.