MA2051 - Ordinary Differential Equations
Solutions to Sample Exam #1 - A96
Originally Given 1993 A Term
-
1
-
-
A)
-
A kernels per minute are added.
-
B)
-
Kernels are added over
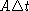 minutes.
minutes.
-
C)
-
Let k be the fraction of the kernels which pop each minute. Then
k n(t) kernels per minute are popping out of the kettle.
-
D)
-
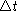 kernels pop out of the kettle
in
kernels pop out of the kettle
in 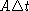 minutes.
minutes.
-
E)
-
Conservation of popcorn:
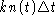 . Divide by
. Divide by
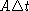 and take the limit
and take the limit
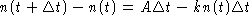 to obtain the differential
equation n' = -kn + A. Add the initial condition
to obtain the differential
equation n' = -kn + A. Add the initial condition
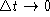 to complete the model.
to complete the model.
-
2
-
(Compare with 3.5/7a.) Start with population
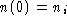 and take an Euler step
and take an Euler step 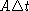 to reach
population
to reach
population 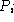 :
:

Solve to find 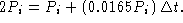 years to double the
world's population. (Just three generations!)
years to double the
world's population. (Just three generations!)
- (Compare with 3.2/3, 3.8/5, 3.11/25.)
-
3
-
-
A)
-
To find a particular solution, use undetermined coefficients.
Begin with
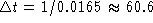 .
Substitute in y' = ky - 2t and collect coefficients of powers
of t to find A - kB = 0, kA - 2 = 0. Hence,
A = 2/k,
.
Substitute in y' = ky - 2t and collect coefficients of powers
of t to find A - kB = 0, kA - 2 = 0. Hence,
A = 2/k, 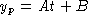 , and
, and
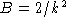 .
.
To find a homogeneous solution, solve y' = ky by separation
of variables or characteristic equations to find
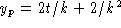 . Hence, a general solution
is
. Hence, a general solution
is 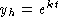 .
.
-
B)
-
Solve
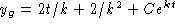 to find C = 1.
The solution of the initial value problem is
to find C = 1.
The solution of the initial value problem is
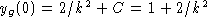 .
.
-
C)
-
Given the particular solution Z(t), use the homogeneous
solution from above to write
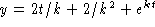 . To solve the
initial value problem, solve
. To solve the
initial value problem, solve 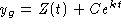 to
find C = 10. The solution of the initial value problem is
to
find C = 10. The solution of the initial value problem is
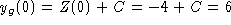 .
.
-
4
-
(Compare with 4.2/4a, 4b, 11a, 11b, 19b.)
-
A)
-
Solve
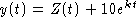 to find the single steady
state
to find the single steady
state 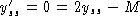 .
To assess stability, examine a direction field diagram, graph
solutions in the vicinity of
.
To assess stability, examine a direction field diagram, graph
solutions in the vicinity of 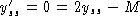 ,
or use the following stability analysis.
,
or use the following stability analysis.
-
B)
-
Consider a perturbation p(t) of the steady state. Let
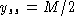 . Substitute in
y' = 2y - M to find p' = 2p or
. Substitute in
y' = 2y - M to find p' = 2p or
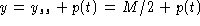 . Since the perturbations
grow, the steady state
. Since the perturbations
grow, the steady state 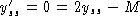 is unstable.
is unstable.
© 1996 by Will Brother.
All rights Reserved. File last modified on September 16, 1996.
 minutes.
minutes.
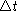 kernels pop out of the kettle
in
kernels pop out of the kettle
in 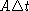 minutes.
minutes.
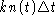 . Divide by
. Divide by
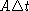 and take the limit
and take the limit
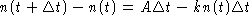 to obtain the differential
equation n' = -kn + A. Add the initial condition
to obtain the differential
equation n' = -kn + A. Add the initial condition
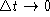 to complete the model.
to complete the model.