MA2051 - Ordinary Differential Equations
Test 1 - Make-Up 1 - Solutions - A96 








    


    

  1. 

    

    
A

     Since the velocity of the falling elevator is negative and 
    the force of the brake must point in the opposite direction,  tex2html_wrap_inline53 .

    
B

    
 Let m be the mass of the elevator.  From 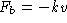 tex2html_wrap_inline57  and 
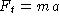     tex2html_wrap_inline59 , obtain mv' = -mg - kv or v' = -g - kv/m.  
    Add the initial condition 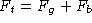 tex2html_wrap_inline65  to complete the model.

    
C

    
 Elevator should cease to accelerate -- reach its maximum 
    (downward) velocity -- when the force of gravity is balanced by the 
    force of the brake.

    
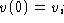    To find  tex2html_wrap_inline67 , suppose it is constant.  Substitute in the 
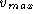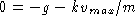    DE to obtain  tex2html_wrap_inline69  or  tex2html_wrap_inline71 .  
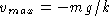    Indeed, the upward force  tex2html_wrap_inline73  of the brake balances the 
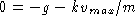    downward pull -mg of gravity.  A designer can reduce  tex2html_wrap_inline71  by half by doubling the friction coefficient k in 
    the brake or by reducing the mass m of the elevator by half.

    
D

    
 To solve the DE, use 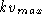 tex2html_wrap_inline83 .  Use 
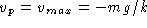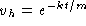    characteristic equations with v' + kv/m = 0 to obtain  tex2html_wrap_inline87 .  Hence,  tex2html_wrap_inline89 .  Choose C from 
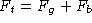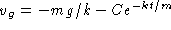     tex2html_wrap_inline65  to obtain  tex2html_wrap_inline95 
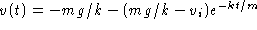    or  tex2html_wrap_inline97 .

    
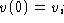    Observe that v never reaches  tex2html_wrap_inline67  except in the 
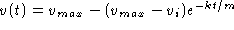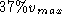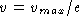    limit of infinite time.  For the time to  tex2html_wrap_inline103 , set  tex2html_wrap_inline105  and let  tex2html_wrap_inline107 .  
    Then

    
        v_max/e &= &v_max ( 1 - e^-kt/m ) 
     
        e^-kt/m &= &1 - 1/e 
     
        t &= & -(m/k) (1 - 1/e ) = (m/k) ( 1 - (e - 1) 
            )

    

    

    

    
2

    
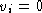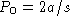 Apply Euler with unknown step  tex2html_wrap_inline109  from  to  tex2html_wrap_inline113 : 
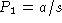 tex2html_wrap_inline115 .  Solve to find 
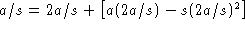 tex2html_wrap_inline117 , which has units of time since a has units of inverse 
time ( 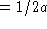tex2html_wrap_inline121 ).  This approximation underestimates the true value 
because 1) the exact solution is concave up and decreasing for a/s < 
P, 2) P reaches a/s only in the limit of infinite time.

  2. 

    

    3. 

    

    

    
3

    

  3.  Substitute 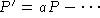 tex2html_wrap_inline129  constant into the DE to obtain 
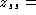     tex2html_wrap_inline131 , a glaring contradiction.

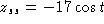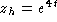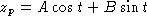  4.  Applying characteristic equations to z' - 4z = 0 yields  tex2html_wrap_inline135 .  Undetermined coefficients starting with  tex2html_wrap_inline137  leads finally to  tex2html_wrap_inline139 .
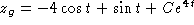    Choosing C so that  tex2html_wrap_inline143  gives the IVP solution 
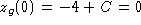     tex2html_wrap_inline145 .

    

  5. 

    

    6. 

    

    

    
4

    

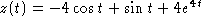  6.  By superposition,  tex2html_wrap_inline147 .

  7.  Since 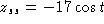 tex2html_wrap_inline135  solves z' = 4z,  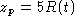tex2html_wrap_inline153 .  Choosing C so that  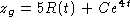tex2html_wrap_inline157  gives 
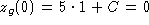    the IVP solution  tex2html_wrap_inline159 .

    

    8. 


    
  
    
    
    
© 1996 by     Will Brother.
All rights Reserved. File last modified on September 27, 1996.