- A
- rV l/min
- B
- H l/min
- C
-
The change in the amount of water in the tank from t to
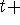 is the amount
added over less the amount lost.
Change over
is the amount
added over less the amount lost.
Change over 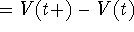 .
Amount added
.
Amount added 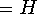 .
Amount lost
.
Amount lost 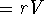 .
Conservation requires
.
Conservation requires
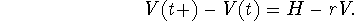
Divide by , take the limit as
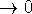 to obtain
dV/dt = -rV + H. (Not required: for a complete model, add the
initial condition
to obtain
dV/dt = -rV + H. (Not required: for a complete model, add the
initial condition 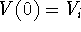 .)
.)
- D
-
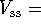 constant yields
constant yields 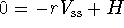 .
Hence, there is a single steady state
.
Hence, there is a single steady state 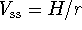 .
.
Since
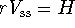 , this steady state represents a balance
between leakage at the rate
, this steady state represents a balance
between leakage at the rate 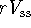 l/min and additions at
the rate H l/min.
l/min and additions at
the rate H l/min.
- E
-
One stability argument: study solutions of the form
V(t) = H/r + p(t), where p is small initially. Substituting in
V' = -rV + H and simplifying yields p' = -rp. Since
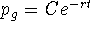 , the perturbation p decays and
, the perturbation p decays and 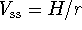 is
stable.
is
stable.
Another argument: Using characteristic equations and undetermined coefficients, the general solution of V' = -rV + H is
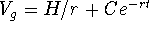 . The arbitrary constant C is determined
by the initial condition. Hence, regardless of the initial state,
every solution of V' = -rV + H decays to
. The arbitrary constant C is determined
by the initial condition. Hence, regardless of the initial state,
every solution of V' = -rV + H decays to 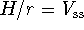 .
.